Eclipse Predictions
All right, so astronomers are CERTAIN that there will be a total eclipse of the Sun on April 8, 2024. They’ve known this for years – even for decades. In fact, astronomers have known there will be an eclipse on this date for at least a few hundred years! But how? How is it possible that scientists can tell us in advance what time the Moon will completely cover the Sun from any location in the path of totality, and they can do it with accuracy down to the second?
It seems impossible – but even thousands of years ago, people studied the night sky very intently. They charted the motions of the stars, the Sun, Moon and planets very carefully. They may not have had Calculus to help them with their calculations, but that didn’t stop them from being able to come up with a means of very accurately predicting the positions of all these bodies with great accuracy. They also logged enough data to detect patterns in the various events that were of interest to them. The ancient Greeks were well aware of the Saros cycle for eclipses, and they used this to predict eclipses with great accuracy. The famous Antikythera Mechanism incorporated eclipse predictions into its many astronomical uses.
Fast forward to 1824. We now have at our disposal a body of very robust mathematics, and many brilliant astronomers and mathematicians who could put these tools to use. In Germany, an accountant named Friedrich Wilhelm Bessel became interested in eclipses, and invented an amazingly simple, amazingly accurate means of predicting eclipses, the essentials of which are still in use today. His method was pure genius, because it simplified the calculations immensely (making them “possible”), while not losing any accuracy at all. It was mathematical magic, and with only a few refinements (as well as some process improvements to make the formulas more amenable to computation using computers), it is the method we still use to this day!
Bessel’s simplification
It is very complicated – and may be impossible – to solve a set of mathematical equations when there are lots of variables. When so many objects (like the Sun, the Moon, and the Earth) are moving around constantly, and when there are so many factors that can influence where the Moon’s shadow is going to be in space at any given point in time, it can be practically impossible to get any accuracy at all in our predictions. The math is certainly beyond anything simple that we learn in high school (or even in college – even if one gains an undergraduate degree in Mathematics!).
Bessel’s brilliant key to solving the eclipse prediction problem was to transform the complicated situation into an easier one that we can find a simpler solution for. And then, if we can break up that solution into steps, so that we’re not solving multiple problems at once, that will streamline the process even further. Bessel may not have been an academician, but he was right on target with ideas to simplify the problem of eclipse calculations! His simplification of the geometry of the situation is nothing short of brilliant, as you’ll agree once you see it in action.
First (without realizing the joy of legitimization this act might bring to a certain subset of future Earth inhabitants), Bessel flattened the Earth. That’s right, he considered an Earth that was not spherical but flat (have we opened a can of worms here?), and thought about how to calculate the umbral path on this flattened Earth. But to do that, he needed to consider a very “special” flat Earth. Bessel imagined a huge flat plane lying in space, with the conical umbra of the Moon scraping across it during an eclipse:
As the Moon moved, the imaginary flat Earth-plane rotated slightly along with it, so that the umbra was at all times hitting this “Earth” in a perfectly perpendicular fashion. This simplified the situation so much that the entire shadow path could be calculated using only a few orbital parameters, mostly based on the movement of the Moon.
By keeping the plane of the now-flat Earth (which Bessel called the “fundamental plane”) perfectly perpendicular to the Moon’s shadow axis, Bessel was assured that the outline of the umbra’s intercept of the fundamental plane would always be a circle. This gives us a very easy-to-describe object traveling over a very easy-to-describe plane, using only parameters that involve the movement of the Moon. While it is still true that finding the position of the Moon in the first place was still ultra-complicated, there were known algorithms to do that. Bessel was only taking as input some values from those lunar position calculations that were already being done (called the “Besselian Elements” of the eclipse), and then applying them to his simplified eclipse situation. The eclipse calculations can then, in fact, be done with nothing more than high school trig! Bessel’s simplification was pure genius.
(Note to purists: The lunar shadow outline on the fundamental plane will not be a perfect circle, because the Moon itself is not an exactly perfect sphere. However, it is so close that we lose practically nothing at all by making that assumption. And if we want to introduce that level of accuracy into the calculations, we can do so with math that is only slightly more complicated. We just use an ellipse [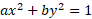
] instead of a circle [
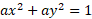]), and note that the Moon’s flattening is 1/900. In what follows, we will call it a circle, and leave it at that.
But the Earth isn’t flat. It’s really a sphere, right? And it’s not even a true sphere at that – it’s an “oblate spheroid”, as we know from actual measurements and some basic physics. And by the way, the study of the shape of the Earth is called “Geodesy”, and it’s an amazingly wonderful body of work. There are so many ramifications to Geology, Cartography, Astronomy, Aeronautics, Ballistics, and even things like GPS calculations – it’s one of those topics that you’d never think about being something that people could study! (“What do you do for a living?” “I study the shape of the Earth.” “Really? That’s…nice. I thought it was ‘round’?”) And the Earth’s shape isn’t constant; it’s changing slightly due to the rebounding of the crust from being compressed during the last Ice Age. Cool stuff!
Because the Earth is a sphere, the outline of the Moon’s shadow on the Earth’s surface is not going to be perfectly round. And while we’re at it, how will we be able to tell what part of the Earth is in the shadow at any given moment? Did Bessel’s simplification make things somehow TOO simple?
Nope. You see, we know with high accuracy where that shadow’s outline lies on the fundamental plane at any given time. We also know (via some very common spherical trigonometry formulas – or at least, as common as spherical trig ever gets!) how to “project” that lunar shadow circle on the fundamental plane up to the surface of the real Earth, thereby converting the coordinates of that shadow’s position on the plane into real latitude and longitude coordinates we can use with a round Earth. This assumes we know what part of the Earth is lying directly above that shadow’s spot on the fundamental plane; but since we know the exact time represented by our calculation (we choose it to be whatever we want), we know how far the Earth has moved in its daily rotation. A big tweak due to the equation of time (based on what day of the year it is), and a little tweak due to an ever-changing value of Delta-T, and we have our answer!
A complication arises due to the fact that the Earth’s flattening is not constant, but depends on the latitude under consideration. So if you want to know where that fundamental plane shadow outline projects up onto the real Earth’s surface, you have to know the latitude of where that projection will end up at. But you don’t know that exactly where that is UNTIL you project it! And if you assume it to be some value, that value will end up being altered by the difference in flattening between where you thought it was and where it actually is.
We therefore have two variables to solve for, but only one equation governing the situation. In this case, we are forced to mathematically “iterate” to find a solution. Iteration involves making an educated guess at the solution, then seeing what the changes in that solution are, once we plug the values into the model for the real Earth. We then take those new values and plug THEM back into the equations, and see where that lands us. (Those of you who slugged through Calculus might remember a thing called “Newton’s method” of iteration to find zeros of a function? It’s basically the same thing, in somewhat fancier clothes.) We continue in this manner until we’ve found the exact value – a value that doesn’t change materially (and we determine the level of that precision) when we continue to plug it back into the iteration process.
We do that for lots of points around the circumference of that shadow-outline circle on the fundamental plane, to project each of them up to the surface, and we will end up drawing a somewhat elliptical-shaped thing lying on the surface of the real Earth. That’s our shadow outline for that exact moment during the eclipse. If we do that for every moment that the Moon’s shadow is scraping over the Earth, then we will have drawn a pretty good map of the umbral outline over the surface of the Earth - the "path of totality"! It will be accurate for all normal eclipse-viewing activities – though there are ways to make it even better! (Nerd alert! We’ll go over those methods on another page.) And, sorry to say for flat-Earthers, if we do this based on our knowledge of the exact value of the flattening of the Earth that we've determined through the science of geodesy, we come up with values that are found in practice to be literally perfect on eclipse day. Yup, we’ve assumed a round Earth, and we’ve obtained values that match our observations to the second. That’s pretty good evidence that we’ve got the Earth’s curvature correct!
Similar mathematical processes exist for finding the eclipse circumstances at a given location, for finding the northern and southern limits of the path, for finding the path width, the points where the path begins and ends, the maximum duration of totality for any point along the path, the first point on the Earth where the umbra touches, and the last point where it leaves, and all of this same stuff for the places on Earth where the eclipse is just partial. Everything starts with Bessel’s simplification, and the results come out the back end of the process, ready to be used by eclipse chasers around the world! Is it “right”? Well, it gives results that you can bank on, to the second, eclipse after eclipse. It is repeatable, predictable, and verifiable. So yeah, I guess you could call that “right”… :-)
Besselian Elements
Central to all eclipse predictions are the Besselian Elements. This set of numbers (for example, this set of Besselian Elements for the 2024 total eclipse) defines the position and motion of the Moon, as well as the geometry of the Earth-Moon-Sun system for a given time (namely, a time around mid-eclipse!), and provides the basic information needed to plug into Bessel’s computational algorithm. To do these calculations, everything begins with knowing the very accurate parameters of the orbits and motions of the Moon and the Earth. The Elements are calculated from those parameters, and the details of those calculations are well beyond the scope of this site.
The difficulty of obtaining these parameters should not be underestimated, as the position of the Moon is one of the more difficult calculations among the more common celestial mechanics values. (If you have a graduate math or physics degree, you will understand this already; if not, then the math is likely something you will need to work your way up to – but believe us, it’s tough!)
Fortunately, there are individuals who spend significant portions of their careers calculating these orbits (Fred Espenak is one of these intrepid individuals, and his work has earned him the well-deserved moniker "Mr. Eclipse"). The rest of us piggyback off their work to obtain highly accurate eclipse calculations! The Besselian Elements for each eclipse are very well-known in advance, and very small adjustments are made only occasionally. Changes to the Elements that occur within a decade or so of each eclipse will not throw off the predictions by more than a few seconds – and this is well within the margin of error of timing the start and end of totality due to edge effects. This is why we can be very certain that the values we have are sufficient to allow for predictions accurate enough for the overwhelming majority of eclipse chasers - and it's why astronomers have known for centuries that there WILL be an eclipse on April 8, 2024!
Oblateness of the Earth
The Earth is not a perfect sphere! Because the earth is spinning, it bulges slightly at the equator. This causes the equatorial radius and the polar radius to vary from each other slightly (by about 13 miles!). If you were to draw two diagrams to scale – one of the oblate Earth and one of a perfectly round Earth – you would NOT be able to tell the difference. This flattening, as it’s called, is not very much – only about 1 in 298 or so – but it’s enough that we need to take it into account for eclipse predictions.
We’ve written an entire page devoted to Delta-T. Because it is a critical value for predicting local circumstances of the eclipse, we suggest you give that page a good read!
Moon’s limb – edge effects
We’ve discussed edge effects in another topic, explaining why eclipse predictions to the nearest tenth of a second aren’t really useful for the average observer. It is an entire discussion all on its own!
How do we know that Bessel’s method works?
Astronomers have used Bessel’s method to predict eclipses since he first invented it in the early 1800s. It is true that we have refined our knowledge of the Moon’s motion, and that we have developed more sophisticated ways of telling exact time based on the very small fluctuations in the Earth’s rotation. We can measure Delta-T very accurately, and we have a good deal of confidence in our predications of it in the short- and medium-term future. We also have the LRO map of the Moon’s limb to allow us to be very precise with the timings and appearance of Baily’s Beads. But these are slight refinements to the precision of the predictions; they have not, for example, caused the exact DAY of any given eclipse to change!
When we use these methods, we discover that the Sun and the Moon line up perfectly, eclipse after eclipse, from any location we choose, exactly as we have predicted. Some people, even today, will argue that the Earth is flat, or that the eclipse cannot possibly progress from West to East, or that it is “suspicious” that the 2017 eclipse path crossed the US from NW to SE, while the 2024 eclipse travels from SW to NE. Conspiracies aside (NASA, of course, having absolutely nothing better to do than to try to confuse the general public regarding the timings of an eclipse!), we see that this predictability is a reason to have faith in the method. Even if you believe the Earth is flat, you cannot argue with the fact that observers stationed in the predicted path of totality will witness all eclipse events happening EXACTLY as predicted by the model. So, does that mean the model is “true”? Well, if truth is represented by 100% accuracy and predictability over numerous experiments, then that fits this particular definition. Even if the models aren’t “true”, they have been proven completely accurate and dependable for eclipse observing – so we can leave the question of “truth” to the philosophers!
So, you can be sure that we’ve got the path correct, and that if you make the effort to position yourself within the path of totality, AND if you have good weather on eclipse day, you WILL be treated to one of the most amazing sights you can ever hope to see. The 2024 eclipse WILL happen, just as the 2017 eclipse did. And it will happen WHEN and WHERE it was predicted to happen. Do you have to concern yourself with all this technical detail? NO – you only have to trust that we who have seen so many of these things are trying to get OURSELVES into the path of totality, and we’d like to convince you to come with us to the path, so you can see totality too! There’s really no motivation other than that! So… get to the path! And enjoy the eclipse safely!
