Diagrammes d'astronomie interactifs
Observez les mouvements du Soleil, de la Lune et de la Terre pour mieux les comprendre!
Voici quelques diagrammes qui pourront vous aider à mieux comprendre les mouvements du Soleil, de la Lune et de la Terre. Pour chacun d’eux, vous trouverez une brève description du phénomène à observer.
La plupart des diagrammes vous permettent de contrôler le mouvement des objets dans l'image à l’aide de barres de défilement. Pour un meilleur angle de vue, utilisez votre souris pour tourner l'image et zoomer sur celle-ci.
Mouvements quotidiens du Soleil dans le ciel
On va vous expliquer pourquoi le Soleil peut être observé à des endroits différents dans le ciel selon le moment de l’année.
On va aussi vous montrer la trajectoire quotidienne du Soleil à partir de différents emplacements sur la Terre.
Consultez les instructions du diagramme 1Refermer les instructions
Diagramme 1 :
Mouvement quotidien du Soleil dans le ciel
Ce que vous pouvez observer :
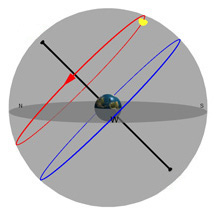
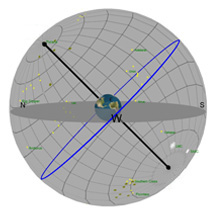
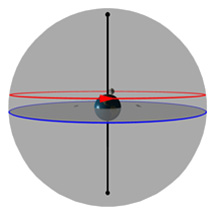
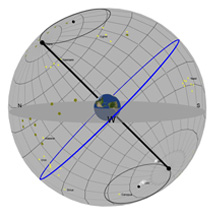
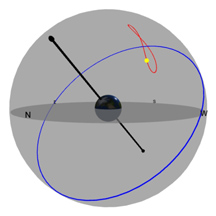
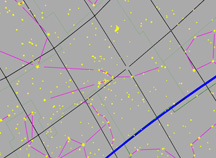
La plaque ronde grise dans le centre de la sphère représente l’horizon comme vous pourriez le voir si vous vous teniez debout sur la Terre à la latitude indiquée par le curseur de défilement « Latitude ». Imaginez-vous en train de vous tenir debout au-dessus de cette sphère qui représente la Terre. On a ajouté un petit bonhomme vert, un « observateur », pour vous montrer où vous vous trouveriez.
Le cercle rouge représente la trajectoire du Soleil à travers le ciel à un jour donné (cette trajectoire peut changer d’une journée à l’autre). Le cercle bleu représente la projection de l'équateur de la Terre dans l'espace. (celle-ci ne change jamais*!). La petite boule jaune dans le ciel est le Soleil tel qu'il apparaît depuis la Terre.
Le pôle noir qui traverse la Terre est un pôle imaginaire autour duquel la Terre tourne. Si nous étendons ce pôle imaginaire jusqu'à l'espace, il crée ce que nous appelons le Pôle Céleste Nord (PCN) au nord, et le Pôle Céleste Sud (PCS) au sud.
*(Voir les autres diagrammes qui traitent de la « Précession »!)
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l'écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l'ensemble du diagramme.
Montrer l'observateur
Si vous cochez cette case, vous verrez un observateur, un petit bonhomme vert, se tenir sur le dessus de la Terre.
L'horizon qu'on a tracé avec le disque gris et le cercle bleu représentent l'horizon que cet observateur pourrait voir.
Décochez la case pour cacher l'observateur.
Réinitialiser l'horizon
Il n'est pas toujours facile d'obtenir la vue exactement comme on le souhaite. Utilisez ce bouton pour réinitialiser l'horizon.
Tourner la terre
Vous pouvez tourner la Terre pour placer l'observateur exactement à l'endroit où vous vous trouvez maintenant.
Ceci vous permettra de voir les objets dans le ciel exactement comme ils apparaissent là où vous êtes présentement.
Le nombre qui apparaît à la droite de cette barre de défilement représente la longitude de l'endroit où se trouve l'observateur.
Latitude
Déplacez le curseur près de votre latitude approximative sur Terre. La Terre s'inclinera lorsque vous la déplacerez.
Si vous vous « déplacez » vers des endroits comme l'hémisphère sud, l'équateur et les pôles Nord ou sud,
vous verrez un mouvement quotidien du Soleil TRÈS différent de ce que vous voyez habituellement dans le ciel.
Le Soleil n'ira jamais au-delà de l'angle de 23,5° du nord au sud, puisqu'il s'agit de l'angle maximal d'inclinaison de la Terre.
Déclinaison
Déplacez le curseur pour simuler la déclinaison (la « latitude » céleste) du Soleil. Lorsque vous le déplacez, la trajectoire du Soleil dans le ciel montera et descendra.
Le Soleil sera à environ 23,5° de déclinaison nord le 21 juin de chaque année, et à environ 23,5° de déclinaison sud le 21 décembre.
Il sera à environ 0° le 21 septembre et le 21 mars.
En d'autres mots, en déplaçant le curseur, vous fixez approximativement le jour de l'année.
Vitesse du Soleil
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes. Elle vous permet de déplacer les objets dans les diagrammes à des vitesses variables.
Cliquez et maintenez le curseur enfoncé. Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement.
Relâchez-le pour qu'il revienne vers la gauche et arrête le mouvement.
Ce curseur vous permet de contrôler le temps, et de déplacer le Soleil dans le ciel.
Temps
Déplacez ce curseur pour simuler le mouvement du Soleil dans le ciel durant une journée. Ce mouvement est dû à la rotation de la Terre.
L'heure indiquée est l'heure solaire locale approximative.
Ce que vous pouvez apprendre :
- Vous comprendrez pourquoi le Soleil se lève et se couche toujours EXACTEMENT à l'Est ou à l'Ouest les premiers jours du printemps et de l'automne.
- Vous verrez pourquoi le Soleil ne se lève parfois jamais ou ne se couche jamais lorsque vous êtes près d'un des deux pôles.
- Vous verrez pourquoi le Soleil est si haut dans le ciel près de l'équateur à midi et pourquoi il se lève et se couche presque toujours à 6 heures ou 18 heures.
- Vous comprendrez pourquoi les heures de coucher et de lever du soleil changent autant pendant l'année si vous êtes plus au nord qu'à environ 35° (ou plus au sud qu'à 35° sud!)
- Vous pouvez voir pourquoi, quand vous êtes dans l'hémisphère Sud, vous devez vous tourner vers le Nord pour voir le Soleil se déplacer dans le ciel - et pourquoi on a l'impression qu'il se déplace dans le ciel dans le sens opposé de ce qu'on peut voir dans l'hémisphère Nord!
Mouvements quotidiens de la Lune dans le ciel
On va vous montrer pourquoi la Lune est parfois vraiment haute ou vraiment basse dans le ciel.
On va aussi vous montrer les différentes trajectoires quotidiennes de la Lune à partir de différents endroits sur la Terre.
Consultez les instructions du diagramme 2Refermer les instructions
Diagramme 2 :
Mouvement quotidien de la Lune dans le ciel
Ce que vous pouvez observer :
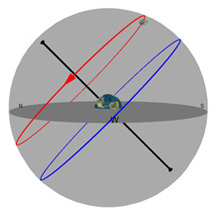
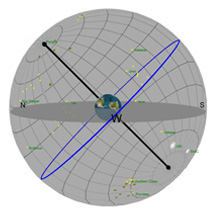
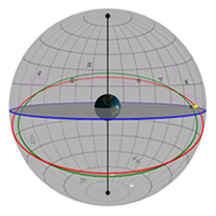
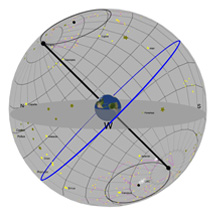
Comme dans le diagramme précédent, la plaque ronde grise dans le centre de la sphère représente l’horizon comme vous pourriez le voir si vous vous teniez debout sur la Terre à la latitude indiquée par le curseur de défilement « Latitude ». Imaginez-vous en train de vous tenir debout au-dessus de cette sphère qui représente la Terre. On a ajouté un petit bonhomme vert, un « observateur », pour vous montrer où vous vous trouveriez.
Le cercle rouge représente la trajectoire du Soleil à travers le ciel à un jour donné (cette trajectoire peut changer d’une journée à l’autre). Le cercle bleu représente la projection de l'équateur de la Terre dans l'espace. (celle-ci ne change jamais*!). La petite boule grise dans le ciel est la Lune telle qu'elle apparaît depuis la Terre.
*(Voir les autres diagrammes qui traitent de la « Précession »!)
Si vous regardez attentivement, on s’est arrangé pour que la Lune montre toujours la même face par rapport à la Terre. En effet, dans la vie réelle, il y a une face de la Lune qu’on ne voit jamais depuis la Terre. Certains disent qu’il s’agit du côté obscur de la Lune, mais il vaut mieux alors l’appeler le côté éloigné de la Lune. En effet, cette face ou ce côté de la Lune reçoit autant de lumière du Soleil que le côté visible depuis la Terre.
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Montrer l'observateur
Si vous cochez cette case, vous verrez un observateur, un petit bonhomme vert, se tenir sur le dessus de la Terre.
L'horizon qu'on a tracé avec le disque gris et le cercle bleu représentent l'horizon que cet observateur pourrait voir.
Décochez la case pour cacher l'observateur.
Réinitialiser l’horizon
Il n’est pas toujours facile d’obtenir exactement la vue que vous voulez. Utilisez ce bouton pour réinitialiser l’horizon.
Tourner la terre
Vous pouvez tourner la Terre pour placer l'observateur exactement à l'endroit où vous vous trouvez maintenant.
Ceci vous permettra de voir les objets dans le ciel exactement comme ils apparaissent là où vous êtes présentement.
Le nombre qui apparaît à la droite de cette barre de défilement représente la longitude de l'endroit où se trouve l'observateur.
Latitude
Déplacez le curseur de défilement près de votre latitude approximative sur la Terre. La Terre s'inclinera lorsque vous la déplacerez.
Si vous vous « déplacez » vers des endroits comme l’hémisphère Sud, l’équateur ou les pôles Nord ou Sud,
vous pourrez simuler les mouvements quotidiens de la Lune comme on peut les observer depuis ces endroits!
La Lune peut se déplacer plus loin dans le ciel au Nord et au Sud que le Soleil le peut, parce que l’orbite de la Lune est inclinée de 5° de plus que la trajectoire empruntée par le Soleil. Quand les deux sont à leur maximum, vous obtenez un peu plus de 23° pour le Soleil, et un peu plus de 5° pour la Lune - ce qui fait un total de près de 29°.
Déclinaison
Utilisez la barre de défilement pour simuler la déclinaison (la « latitude » céleste) de la Lune.
Alors que vous déplacerez le curseur dans la barre de défilement, la trajectoire de la Lune dans le ciel va monter et descendre. Alors que la Lune effectue son orbite autour de la Terre à chaque mois, sa déclinaison change drastiquement.
On ne peut pas non plus prédire quelle sera la déclinaison exacte de la Lune pour un jour précis du mois – vous devez la calculer ou consulter une table astronomique.
Ce dont vous pouvez être certains, c’est que la Lune passe à travers une très grande variété de déclinaisons (mais jamais toutes les déclinaisons possibles) pendant un mois complet.
Vitesse de la Lune
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes. Elle vous permet de déplacer les objets dans les diagrammes à des vitesses variables.
Cliquez et maintenez le curseur enfoncé. Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement.
Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Ce curseur vous permet de contrôler le temps, et de déplacer la Lune dans le ciel.
Temps
Déplacez ce curseur pour simuler le mouvement du Soleil dans le ciel durant une journée. Ce mouvement est dû à la rotation de la Terre.
L'heure indiquée est l'heure solaire locale approximative.
Ce que vous pouvez apprendre :
- Vous pouvez voir pourquoi la Lune est parfois vraiment haute dans le ciel, et parfois vraiment basse – et ceci ne dépend pas de la phase de la Lune, ou de où vous vous trouvez sur la Terre!
- Vous pouvez voir pourquoi parfois la Lune ne se lève ou ne se couche jamais quand vous êtes près du Pôle Nord ou du Pôle Sud.
- Vous pouvez voir pourquoi, dans l’hémisphère Nord, la Lune apparaît comme étant « penchée » sur son côté droit quand elle se lève, et penchée sur son côté gauche quand elle se couche. Dans l’hémisphère Sud, c’est le contraire.
- Vous pouvez voir pourquoi, quand vous êtes dans l'hémisphère Sud, vous devez vous tourner vers le Nord pour voir le Soleil se déplacer dans le ciel - et pourquoi on a l'impression qu'il se déplace dans le ciel dans le sens opposé de ce qu'on peut voir dans l'hémisphère Nord!
Les phases de la lune
Découvrez pourquoi la Lune a-t-elle des phases!
Consultez les instructions du diagramme 2aRefermer les instructions
Diagramme 2a :
Les phases de la Lune
Dans ce diagramme, nous voyons pourquoi est-ce que la Lune apparaît dans différentes « phases » pendant le mois.
Depuis la Terre, nous voyons la Lune se déplacer lentement dans le ciel, d'ouest en est, au cours du mois. Ce mouvement est dû à son orbite autour de la Terre. Ce n'est PAS la même chose que le mouvement que la Lune effectue de l’est vers l’ouest chaque nuit en raison de la rotation de la Terre!
Tout au long de son orbite, la Lune présente toujours la même face à la Terre, grâce à ce qu'on appelle la « rotation synchrone ». Mais comme la moitié qui fait face au Soleil change tout le temps, de notre point de vue on dirait que c’est la forme de la Lune elle-même qui change. Comme ces changements sont répétitifs et prévisibles, on les a nommés « phases » - et c'est comme ça qu’on continue de les appeler aujourd'hui.
Ce que vous pouvez observer :
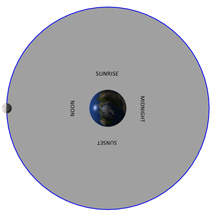
Nous avons simplifié ce diagramme autant que possible pour vous montrer en gros comment les phases fonctionnent. Dans le diagramme, vous êtes positionnés au -dessus du Pôle Nord ou du Pôle Sud de la Terre, et la Lune est sur une orbite circulaire autour de la Terre. Le Soleil est loin, tout à gauche du diagramme, et sa lumière éclaire une moitié de la Terre et la face de la Lune orientée vers la Terre.
Vous pouvez contrôler la rotation de la Terre (mais ça ne changera pas la phase de la Lune), et la position de la Lune dans son orbite. Lorsque vous déplacez la Lune, remarquez que chaque jour une section différente de sa surface fait face au Soleil. Comme vous le voyez dans l’encadré, c’est pour ça que la forme de la partie de la Lune éclairée par le Soleil visible depuis la Terre change tous les jours.
La phase que nous observons est provoquée par la différence entre la partie de la surface de la Lune visible depuis la Terre, et la section éclairée par le Soleil.
N’oubliez pas que vous pouvez être situé n’importe où sur la planète ; la phase de la Lune observable depuis la Terre à un moment donné est à peu près pareille pour tout le monde. Toutefois, l'heure de la journée est différente pour chaque observateur sur la Terre, et C'EST ce qui détermine si cet observateur peut apercevoir ou non la Lune!
Noms des phases
Pour décrire plus facilement les phases lunaires, on leur a donné des noms – c’est plus pratique comme ça! Les termes utilisés pour décrire les phases se trouvent dans l'encadré en haut à gauche du diagramme :
Nouvelle Lune
C'est le « point de départ » du mois, lorsque la Lune et le Soleil se trouvent au même endroit dans le ciel. (Un peu plus loin, nous verrons ce
que cette expression « au même endroit » veut dire exactement.) À la nouvelle Lune, impossible d’apercevoir la Lune, elle est située trop près de la
lumière brillante du Soleil!
Pleine Lune
C'est la phase que nous connaissons bien, lorsque la Lune apparaît comme un cercle complet dans le ciel, tellement grosse et lumineuse qu’on pourrait
lire en pleine nuit. La pleine Lune et la nouvelle Lune sont situées à des points opposés de l’orbite lunaire.
La pleine Lune est visible toute la nuit, et elle est à son point culminant dans le ciel vers minuit.
Premier ou dernier croissant
C’est lorsque la Lune apparaît comme un mince croissant. C’est la forme que tous les jeunes artistes en herbe apprennent à dessiner pour représenter la Lune!
La Lune dans cette phase est toujours visible juste après le coucher du soleil, ou juste avant son lever.
Premier ou dernier quartier
Du point de vue d’un observateur sur la Terre, on aperçoit une parfaite demi-Lune et la courbe séparant la section dans l’ombre de la partie éclairée
(une démarcation qu’on appelle le « terminateur » - c’est notre mot préféré en astronomie!) forme une ligne droite.
Le quartier de la Lune est visible tard dans la soirée (premier) ou tôt le matin (dernier).
Gibbeuse
C’est un mot qu’on n’utilise pas tous les jours - en fait, la plupart des gens ne savent pas ce que ça veut dire. C’est comme ça qu’on décrit une Lune de forme
ovale ou « bossue », telle qu’elle apparaît juste avant ou après la pleine Lune.
Croissante
Lorsqu’on dit de la Lune qu’elle est croissante, c’est que sa surface éclairée visible de la Terre augmente à chaque jour. On utilise ce terme pour décrire
la phase gibbeuse qui se produit avant la pleine Lune, on parle alors de Lune gibbeuse croissante.
La Lune croît dans la première moitié du mois, et en général elle est alors visible entre le coucher du soleil et minuit.
Décroissante
L’adjectif « décroissante » indique une réduction de taille et c’est bien ce qui arrive à la surface éclairée de la Lune lorsqu’elle est en phase décroissante.
On utilise ce terme pour décrire la phase gibbeuse qui se produit après la pleine Lune, on parle alors de Lune gibbeuse décroissante.
La Lune décroît dans la deuxième moitié du mois, et en général elle est alors visible dans le ciel entre minuit et le lever du soleil.
L'âge de la Lune
Les astronomes parlent parfois de « l’âge » de la Lune - parfois en heures, parfois en jours. L’âge de la Lune décrit le temps écoulé depuis la dernière
nouvelle Lune. Une « jeune » Lune, âgée de quelques heures, vient tout juste de passer la phase de nouvelle Lune. Ça peut être très difficile d’apercevoir le
croissant de Lune très mince seulement quelques heures après la nouvelle Lune!
Mesurer le point réel des phases
Si vous consultez n'importe quel almanach pour connaître les dates et heures des phases lunaires, vous verrez qu’elles sont indiquées à la minute, voire à
quelques secondes près! Dans la vie quotidienne, une telle précision ne sert pas à grand-chose, mais pour les astronomes c’est important. Il nous faut être
capables de savoir exactement quand les phases se produisent, et chaque fois qu'une action récurrente a lieu, c’est très utile de débuter nos calculs à un
point de départ sur lequel tout le monde est du même avis!
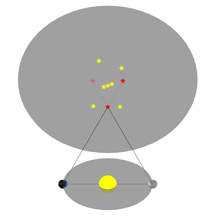
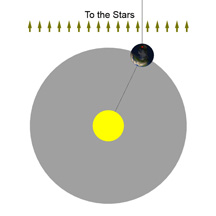
Ça devrait pourtant être facile : il suffit de déterminer quand la Lune et le Soleil se trouvent au même endroit dans le ciel, et voilà le point de départ de la nouvelle Lune. C'est simple, n'est-ce pas ? Eh bien, ce n'est pas si facile que ça. Regardez ce diagramme - il est très exagéré mais il démontre bien le problème :
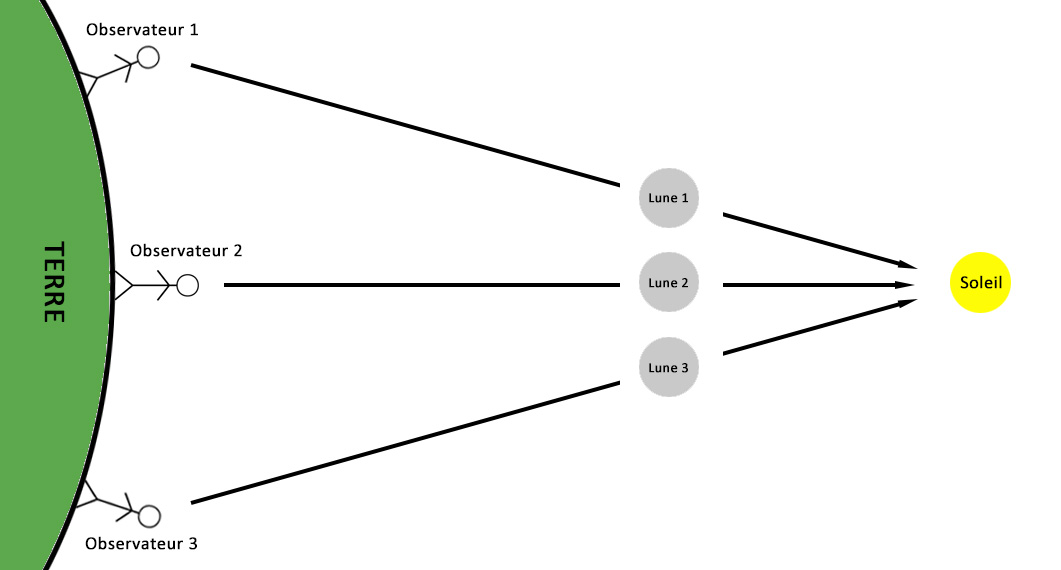
Dans ce dessin, trois personnes observent la Lune depuis différents endroits sur Terre. Chacune d'elles verra la Lune située « au même endroit que le Soleil » à des moments différents, au fur et à mesure que la Lune se déplace sur son orbite.
C’est ça, le problème - la Lune est suffisamment proche de la Terre pour que les gens vivant dans différents endroits voient la Lune et le Soleil « au même endroit dans le ciel » à des moments légèrement différents!
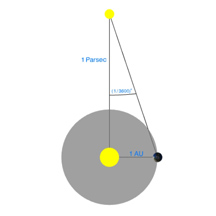
Cet effet de perspective s’appelle le « parallaxe », et nous allons consacrer un diagramme entier à expliquer ce concept.
Pour compliquer encore plus les choses, n’oubliez pas que la Terre (et par conséquent les observateurs aussi) continue de tourner pendant que nos différents observateurs attendent impatiemment que la Lune s'aligne avec le Soleil. C’est donc encore plus compliqué de s’entendre sur une définition précise quand on considère les choses du point de vue des observateurs individuels.
N’oubliez pas non plus que dans ce diagramme, nous avons énormément simplifié les choses en aplatissant la Terre, ce qui nous permet de ne pas tenir compte du fait que les observateurs sont situés à différentes latitudes!
La solution à toutes ces complications est d'éviter que nos calculs dépendent de l’emplacement de l’observateur. Voici donc comment les astronomes déterminent l'heure de la nouvelle Lune : le moment où le Soleil et la Lune sont « alignés », du point de vue de quelqu’un situé au CENTRE de la Terre.
Comme pour à peu près tout en astronomie, il existe des mots sophistiqués pour décrire cette situation, alors autant les apprendre maintenant :
- Le référentiel géocentrique signifie que vous faites vos observations depuis le centre de la Terre. (Bien sûr, c’est impossible d’y aller, mais c'est un point de départ idéal pour des calculs mathématiques. De plus, tout le monde est d’accord sur son emplacement.) Le mot géocentrique signifie « centré sur la Terre ».
- Le référentieltopocentrique signifie que vous faites vos observations de votre position. C’est assez simple de convertir des coordonnées d'observation géocentrique en coordonnées topocentriques, et c'est ce que font les astronomes. (Vous devez d’abord savoir à quelle latitude et longitude se trouve votre observateur, bien sûr.) Le mot topocentrique signifie « centré sur un point ».
Oh, nous avons presque oublié de vous expliquer comment la Lune et le Soleil peuvent sembler être « au même endroit » dans le ciel! Comme les éclipses ne se produisent pas tous les mois (pour des raisons que nous allons explorer dans un autre diagramme), il faut d’abord expliquer ce qu’on veut dire quand on dit que le Soleil et la Lune sont « alignés ». Comme ça, nous serons tous d’accord pour débuter le chronomètre de la nouvelle Lune au même moment dans le temps.
Nous pourrions utiliser plusieurs méthodes différentes pour définir ce moment. Par exemple, nous pourrions utiliser l’instant où la Lune et le Soleil sont à la même hauteur par rapport au sol (altitude), ou à la même distance à l'horizon (azimut). Nous pourrions aussi utiliser le moment du mois où le Soleil et la Lune sont le plus près l’un de l’autre (leur plus petit « écart angulaire »). La difficulté, c'est que ces observations ne seront pas les mêmes pour tous les observateurs. Ça nous oblige à utiliser une définition géocentrique - qui ne dépend pas de l'endroit où se trouve l'observateur.
Nous pourrions utiliser le moment exact où la Lune et le Soleil sont à la même « longitude » apparente dans le ciel. Il y a un terme pour parler de cette « longitude » - on l’appelle « ascension droite ». (On en parlera dans un autre diagramme.) Ce n'est pas une mauvaise idée, mais l'ascension droite est mesurée en utilisant l'équateur terrestre comme référence, et l’équateur change d'orientation lorsque la Terre se déplace autour du Soleil au cours de l'année.
Le meilleur repère à utiliser pour le calcul c’est de définir une autre sorte de « longitude » en utilisant la trajectoire apparente du Soleil dans le ciel au cours d'une année. Cette trajectoire ne change pratiquement pas pendant la vie d'un être humain, voilà pourquoi c’est très utile pour des calculs qui seront comparés sur de longues périodes de temps. On appelle cette trajectoire du Soleil « l’écliptique », et la mesure dont nous avons besoin se nomme la « longitude céleste » (pour la distinguer de la « longitude équatoriale », ou ascension droite). Grâce à ces définitions, nous pouvons dire que le Soleil et la Lune sont au même endroit dans le ciel - et donc que c’est le moment de la nouvelle Lune - au moment où ils ont la même longitude céleste géocentrique.
Félicitations, vous avez tout compris!
Une fois l'heure de la nouvelle Lune établie, on peut simplement utiliser les heures ou les jours ordinaires pour faire avancer « l’âge » de la Lune à travers le reste du cycle des phases jusqu’à ce qu’on en revienne à la nouvelle Lune. Mais n’oubliez pas : le cycle dure à peu près 28 jours, mais pas exactement!
Contrôles :
Jour du mois
Ce curseur permet de déplacer la Lune autour de la Terre au cours du mois. N’oubliez surtout pas que la Lune sera en orbite
dans la bonne direction UNIQUEMENT si vous déplacez la commande de gauche à droite!
Vitesse
Ce curseur permet de déplacer la Lune autour de la Terre dans la bonne direction de son orbite, pendant plusieurs jours.
Vue de l'hémisphère sud/nord
Ce bouton vous permet de vous déplacer vers un point situé directement au-dessus du Pôle Nord ou du Pôle Sud. Si vous avez toujours
vécu ou avez passé la plus grande partie de votre vie dans le même hémisphère, vous remarquerez que la Lune fait les choses suivantes
si vous voyagez dans l’autre hémisphère :
- Elle apparaît « la tête en bas » dans le ciel
- On dirait qu’elle se déplace dans le « mauvais sens » dans le ciel au cours du mois
- On dirait qu’elle se déplace dans le « mauvais sens » dans le ciel au cours de la nuit
- On dirait que les phases apparaissent du « mauvais côté » de la Lune
- Vous devez vous tourner dans une autre direction pour apercevoir la Lune dans le ciel
C’est normal ; c’est parce que vous êtes maintenant dans une région de la Terre qui permet d’observer la Lune d’un angle complètement différent. (Et d'ailleurs, vous aurez l’impression que le Soleil et les étoiles aussi suivent ces mouvements.)
Quand est-ce que les phases de la Lune sont visibles?
Si vous placez la Lune à une certaine phase (en la déplaçant autour de la Terre jusqu'à ce qu'elle apparaisse dans la phase que
vous voulez), vous verrez qu'exactement une moitié de la Terre lui fait face. Par exemple, si vous déplacez la Lune pour qu’elle
soit dans son premier quartier, vous verrez que le terminateur de la Terre – c’est-à-dire la ligne qui sépare le jour de la nuit -
est pointé directement vers la Lune. Si vous faites tourner la Terre, vous verrez que cette partie de la Terre (le long du
terminateur) est en train de voir le coucher du soleil.
Ça veut dire que quel que soit l'endroit où vous êtes sur la Terre, le premier quartier de la Lune est visible d’environ midi à minuit, y compris au coucher du soleil. Et c'est bien ce qu’on constate dans la vraie vie : le premier quartier de la Lune est généralement haut dans le ciel au coucher du soleil.
Lorsque c’est la pleine Lune, elle est à son plus haut dans le ciel nocturne vers minuit tandis que le dernier quartier de la Lune est haut dans le ciel au lever du soleil. Quant à la nouvelle Lune, elle est haute dans le ciel vers midi. C'est pour ça qu’on n’aperçoit jamais cette phase de la Lune; à midi, le Soleil est levé et il est lui aussi haut dans le ciel. Puisque le Soleil apparaît dans le ciel au même endroit que la nouvelle Lune, sa lumière brillante nous empêche de voir la Lune.
Simplifications dans notre diagramme
Nous avons laissé de côté certains éléments qui ne modifient pas les définitions de nos termes, mais dont il est important de tenir
compte dans la vie réelle pour faire des calculs précis. Nous avons ignoré le fait que l'orbite de la Lune n'est pas un cercle parfait
et que la Lune « oscille » en décrivant son orbite (ça veut dire que la partie de la Lune qui nous fait face change un tout petit peu).
Nous avons ignoré l'angle de l'orbite de la Lune par rapport à la trajectoire apparente du Soleil dans le ciel, et nous avons défini une
orbite de 28 jours, alors que ce n’est pas exactement le cas. (En fait, en astronomie il y a CINQ façons différentes de définir un « mois ».
Ces définitions sont toutes légèrement différentes, elles se rapprochent toutes d’une période de 28 jours, et si vous voulez simplement
comprendre les phases lunaires, ces petites différences n’ont aucune importance!)
Quelque chose de plus
Il existe deux calendriers couramment utilisés dans le monde dont les mois sont basés sur les mouvements de la Lune. Bien sûr, vous l’avez
deviné, on les appelle des calendriers « lunaires ». Dans le calendrier musulman, chaque mois débute au moment où l'on aperçoit dans le ciel
le très jeune croissant de lune. Dans l'Antiquité, le calendrier hébraïque utilisait la même définition, mais avec le temps, l'observation
réelle de la Lune a été remplacée par des calculs mathématiques.
Étudier ces deux calendriers en détail dépasse le cadre de notre diagramme. Ces calendriers sont très compliqués, et il faut du temps et des efforts pour les étudier en détail mais ça en vaut vraiment la peine!
Ce que vous pouvez apprendre :
- Vous pouvez voir pourquoi la partie brillante de la Lune semble changer de forme au cours d'un mois.
- Vous pouvez apprendre pourquoi les différentes phases de la Lune ne sont visibles qu'à certaines heures de la nuit.
- Vous pouvez apprendre de nouveaux termes d'astronomie, comme gibbeuse, géocentrique, topocentrique et terminateur.
- Vous pouvez voir que l'apparence et la position de la Lune changent légèrement quand on l’observe depuis différents endroits de la Terre.
- Vous pouvez apprendre que la Lune présente toujours la même face à la Terre.
- Vous pouvez apprendre ce que signifie « l'âge » de la Lune.
- Vous pouvez apprendre qu'il existe différents types de calendriers utilisés à travers le monde.
- Vous pouvez apprendre pourquoi on doit définir les coordonnées dans le ciel de plusieurs manières différentes.
- Vous pouvez voir qu’en astronomie, pour expliquer bien expliquer certaines choses, il faut simplifier autres choses.
Mouvements quotidiens d’une étoile dans le ciel
On va vous expliquer les différents types de mouvements quotidiens possibles pour une étoile située n’importe où dans le ciel, à partir de n’importe quel endroit sur la Terre.
Consultez les instructions du diagramme 3Refermer les instructions
Diagramme 3 :
Mouvements quotidiens d’une étoile dans le ciel
Ce que vous pouvez observer :
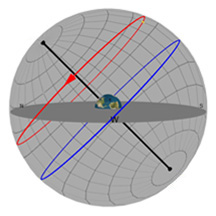
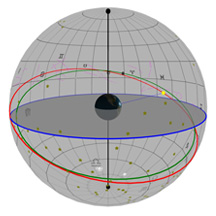
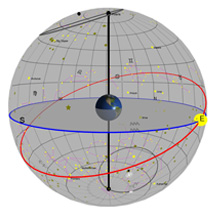
Comme dans les diagrammes précédents, la plaque ronde grise et plate dans le centre de la sphère représente l’horizon comme vous pourriez le voir si vous vous teniez debout sur la Terre à la latitude indiquée par le curseur de défilement « Latitude ». Imaginez-vous en train de vous tenir debout au-dessus de cette sphère qui représente la Terre. On a ajouté un petit bonhomme vert, un « observateur », pour vous montrer où vous vous trouveriez.
On vous a donné ici votre propre étoile! Vous pouvez voir une seule étoile placée en haut dans le ciel, et vous pouvez la déplacer à l’endroit que vous voulez.
On a aussi placé une grille de coordonnées dans le ciel, semblable aux lignes pour la latitude et la longitude que vous pourriez voir sur la Terre. Les astronomes utilisent un système de coordonnées similaire pour décrire les positions dans le ciel. Par contre, là-haut, la latitude est appelée « déclinaison » (dec) et la longitude, l’ascension droite (AD). Chaque objet dans le ciel a une dec et une AD, et pour les étoiles, cet emplacement ne change pas assez pour que vous puissiez le remarquer.
On a créé le tout pour que vous puissiez placer votre étoile à l’endroit que vous désirez en changeant sa déclinaison et son AD – il suffit d’utiliser les curseurs de défilement.
Le cercle bleu représente la projection de l’équateur de la Terre dans l’espace. Le cercle rouge est la trajectoire de votre étoile à travers le ciel à un jour donné. Une fois que vous aurez défini la position de votre étoile, vous allez voir que sa trajectoire ne change jamais pendant le cours d’une année.
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Montrer l'observateur
Si vous cochez cette case, vous verrez un observateur, un petit bonhomme vert, se tenir sur le dessus de la Terre.
L'horizon qu'on a tracé avec le disque gris et le cercle bleu représentent l'horizon que cet observateur pourrait voir.
Décochez la case pour cacher l'observateur.
Réinitialiser l’horizon
Il n’est pas toujours facile d’obtenir exactement la vue que vous voulez. Utilisez ce bouton pour réinitialiser l’horizon.
Tourner la terre
Vous pouvez tourner la Terre pour placer l'observateur exactement à l'endroit où vous vous trouvez maintenant.
Ceci vous permettra de voir les objets dans le ciel exactement comme ils apparaissent là où vous êtes présentement.
Le nombre qui apparaît à la droite de cette barre de défilement représente la longitude de l'endroit où se trouve l'observateur.
Latitude
Déplacez le curseur de défilement près de votre latitude approximative sur la Terre. La Terre s’inclinera lorsque vous l’utiliserez.
Si vous vous « déplacez » vers des endroits comme l’hémisphère Sud, l’équateur ou les pôles Nord ou Sud,
vous pourrez simuler les mouvements quotidiens de la Lune comme on peut les observer depuis ces endroits!
Déclinaison
Contrairement au Soleil et à la Lune, les étoiles peuvent se retrouver à n’importe quel endroit dans le ciel. Certaines étoiles sont très loin au Nord, d’autres sont près de l’équateur,
certaines sont loin au Sud et d’autres se retrouvent partout au milieu de tout cela! On les voit à l’endroit précis où elles sont,
car c’est tout simplement comme ça que la Terre et toutes les étoiles près d’elle se sont alignées à ce moment précis de l’histoire.
Vous pouvez placer votre étoile à l’endroit que vous voulez en utilisant cette fonction!
Mais pourquoi a-t-on parlé des étoiles situées « près de la Terre »? La plupart des gens savent que notre système solaire fait partie de la galaxie appelée la « Voie lactée ». Mais la plupart des gens ne savent pas que chacune des étoiles que vous voyez la nuit dans le ciel est non seulement à l’intérieur de notre galaxie, mais en plus, chacune d’entre elles est située à une distance qui est moins de la moitié de la distance entre la Terre et le centre de notre galaxie! Pour l’expliquer d’une autre façon – CHAQUE ÉTOILE que vous voyez dans le ciel est beaucoup plus près de la Terre que le centre de notre galaxie ne l’est, mais vraiment beaucoup plus près. Vous pouvez complètement oublier la possibilité de voir des étoiles qui sont situées de l’autre côté de notre galaxie! Même par une nuit très noire, les étoiles les plus éloignées que vous pourriez possiblement voir (seulement dans des conditions parfaites) sont situées à moins de 17 000 années-lumière de la Terre. Presque toutes les étoiles que nous pouvons voir sont vraiment, VRAIMENT plus près que ça. Le centre de notre galaxie est à 25 000 années-lumière d’ici! Alors oui, toutes les étoiles que vous pouvez voir sont effectivement – en ce qui concerne notre galaxie – très « près » de nous!
Si vous placez votre étoile à une déclinaison suffisamment élevée, et que vous choisissez une latitude située dans l’hémisphère Nord, alors vous verrez que votre étoile ne se couche jamais, elle reste toujours dans le ciel! (Rappelez-vous, la plaque grise et ronde est l’horizon tel que vous le verriez si vous vous trouviez à la latitude choisie). Si vous placez la déclinaison de l’étoile suffisamment loin au Sud, et que vous choisissez une latitude située dans l’hémisphère Sud, alors vous verrez, encore une fois, que l’étoile là aussi ne se couche jamais! Ces étoiles sont appelées étoiles « circumpolaires », car elles tournent autour des pôles Nord ou Sud et elles sont toujours présentes dans le ciel, elles ne se couchent et ne se lèvent jamais.
Si vous placez l’étoile loin au Nord, et que vous vous placez vous-même loin au Sud, vous verrez qu’il est possible pour vous de ne jamais être en mesure de voir l’étoile! C’est pourquoi, à ce moment précis de l’histoire, les gens qui se trouvent au Canada, s'ils ne quittent jamais le pays, ne pourront jamais voir la Croix du Sud!
Si vous êtes près de l’équateur, alors vous pouvez voir pratiquement chacune des étoiles dans le ciel à un moment ou l’autre de la journée. Enfin, vous le pourriez, si le Soleil, qui est très brillant, n’était pas aussi dans le ciel!
Jouez avec le diagramme un peu, déplacez l’étoile et observez aux alentours. Puis, jouez avec les heures pour que vous puissiez voir l’étoile se lever, se coucher et se déplacer dans le ciel. Ceci vous donnera un bon aperçu de ce qui s’en vient ensuite.
AD
C’est un petit peu plus compliqué à expliquer. À première vue, le fait de déplacer cette étoile à l’aide de ce curseur de défilement ne semble pas faire une grande différence.
Après tout, une fois qu’on a changé l’heure de la journée en utilisant le curseur de défilement « temps »,
l’étoile va se déplacer à travers le ciel pas mal de la même manière que n’importe quelle autre étoile qui a la même déclinaison.
Par contre, si vous regardez attentivement, vous allez voir que la position choisie fait VRAIMENT une différence!
De toute évidence, ce ne sont pas toutes les étoiles dans le vrai ciel qui ont la même AD.
C’est pourquoi certaines étoiles sont hautes dans le ciel à la même heure où certaines autres sont en train de se lever, et que d’autres sont en train de se coucher.
Si vous placez votre étoile à une AD qui fait qu’elle semble se lever à, disons, 6h,
et bien quelqu’un d’autre pourrait placer son étoile à un AD qui fait qu’elle semble se coucher à 6h!
Il y a des étoiles à toutes les AD que vous pouvez imaginer, alors à n’importe quel moment de la journée,
il y a des étoiles qui sont en train de se lever et se coucher – même pendant le jour!
Les étoiles sont toujours dans le ciel – c’est juste qu’on ne peut pas les voir pendant le jour parce que le Soleil est trop brillant. Mais elles sont définitivement là!
Alors, comment savoir où vous devez placer votre étoile? Pour l’instant, il suffit de savoir que vous pouvez utiliser l’AD que vous souhaitez, et nous parlerons plus de cette variable dans de prochains diagrammes. Vous devriez utiliser ce diagramme pour voir comment des étoiles avec des déclinaisons différentes se déplacent différemment dans le ciel.
Vitesse de l’étoile
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes. Elle vous permet de déplacer les objets dans les diagrammes à des vitesses variables.
Cliquez et maintenez le curseur enfoncé. Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement.
Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Cette barre de défilement contrôle le temps, et déplace l’étoile à travers la grille AD/Dec dans le ciel.
Temps
Utilisez cette barre de défilement pour simuler les mouvements de l’étoile dans le ciel pendant une journée. Rappelez-vous que ce mouvement, comme celui de la Lune et du Soleil dans les diagrammes précédents,
est dû à la rotation de la Terre – et non pas aux déplacements réels de l’étoile elle-même! Aussi, l’heure que l’on montre n’a pas une signification précise dans ce contexte-ci –
mais nous reviendrons là-dessus plus tard!
Ce que vous pouvez apprendre :
- Vous pouvez voir pourquoi certaines étoiles sont toujours visibles depuis certaines latitudes.
- Vous pouvez voir pourquoi certaines étoiles ne sont jamais visibles depuis certaines latitudes.
- Vous pouvez voir pourquoi les étoiles semblent se déplacer autour des pôles dans les deux hémisphères.
- Vous pouvez voir pourquoi les étoiles se déplacent dans le sens des aiguilles d’une montre autour du pôle Nord (PCN) et pourquoi elles se déplacent dans le sens inverse autour du pôle Sud (PCS).
- Vous pouvez voir pourquoi, de manière similaire, les étoiles semblent se déplacer de « la gauche vers la droite » quand on fait face au Sud dans l’hémisphère Nord, et pourquoi elles semblent se déplacer de « la droite vers la gauche » quand on fait face au Nord alors qu’on se trouve dans l’hémisphère Sud.
Mouvements quotidiens de plusieurs étoiles dans le ciel
Maintenant, nous allons vous montrer certaines des étoiles, constellations et autres objets célestes les plus célèbres.
Vous allez voir comment ils se déplacent au cours de la journée.
Consultez les instructions du diagramme 4Refermer les instructions
Diagramme 4 :
Mouvements quotidiens de plusieurs étoiles dans le ciel
Ce que vous pouvez observer :
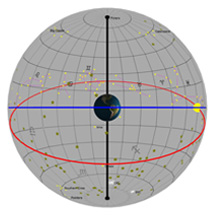
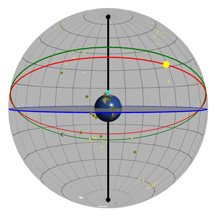
Encore une fois, la plaque ronde grise et plate dans le centre de la sphère représente l’horizon comme vous pourriez le voir si vous vous teniez debout sur la Terre à la latitude indiquée par le curseur de défilement « Latitude ». Imaginez-vous en train de vous tenir debout au sommet de cette sphère qui représente la Terre. On a ajouté un petit bonhomme vert, un « observateur », pour vous montrer où vous vous trouveriez.
On a toujours le cercle bleu, qui représente la projection de l’équateur de la Terre dans l’espace. Par contre, maintenant, nous avons ajouté plusieurs étoiles, des constellations et d’autres objets – et on les a placés à l’endroit où ils se situent réellement dans le ciel, en se basant sur les coordonnées de leur AD et de leur dec. Cette fois-ci, vous ne pourrez donc pas changer les coordonnées des étoiles.
Veuillez prendre en note aussi le fait que toutes les lignes représentant les AD et les dec qu’on a placées dans le ciel sont situées à 15° une de l’autre. Pour la déclinaison (dec), on ne voulait pas avoir trop ou pas assez de lignes pour couvrir l’ensemble de la plage située entre -90° et +90°. De plus, cela correspond au nombre de lignes qu’on voulait vraiment utiliser pour diviser notre grille pour l’AD. Voyez-vous, sur la Terre, on parle de « degrés » autant pour la latitude que pour la longitude. Mais dans le ciel, on n’utilise pas les degrés pour l’AD! C’est plus pratique d’utiliser des heures (on vous expliquera pourquoi un peu plus loin), et lorsqu’on effectue la conversion, on se rend compte qu’une heure d’AD est équivalente à 15° d’arc. (Pourquoi? Les étoiles complètent une boucle de 360° dans le ciel en une journée, ce qui fait 24 heures – donc, 360° divisé par 24 est égal à 15°)!
Vous aviez peut-être même deviné quelle serait notre explication : on utilise des « heures » pour l’AD parce qu’une heure d’AD représente la distance à laquelle une étoile semble se déplacer dans le ciel pendant une heure!
Mesurer des distances dans le ciel
La discussion à propos des « degrés » dans le ciel nous a donné une chance de discuter de quelque chose de très important – comment mesure-t-on les distances entre des objets
dans le ciel? On ne peut pas juste prendre une règle et dire que deux étoiles ont tant de pouces ou de centimètres entre elles!
Les astronomes utilisent des degrés, pareil comme les degrés que vous avez appris à l’école, où un cercle complet a 360° de circonférence.
Si vous tracez une ligne droite dans le ciel à partir d’un point situé sur l’horizon,
en passant par le point directement au-dessus de vous, jusqu’au point opposé sur l’horizon, cela représente 180° d’arc. Une ligne entre l’horizon et le point directement au-dessus de vous représente 90°.
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Montrer l'observateur
Si vous cochez cette case, vous verrez un observateur, un petit bonhomme vert, se tenir sur le dessus de la Terre.
L'horizon qu'on a tracé avec le disque gris et le cercle bleu représentent l'horizon que cet observateur pourrait voir.
Décochez la case pour cacher l'observateur.
Réinitialiser l’horizon
Il n’est pas toujours facile d’obtenir exactement la vue que vous voulez. Utilisez ce bouton pour réinitialiser le diagramme.
Tourner la terre
Vous pouvez tourner la Terre pour placer l'observateur exactement à l'endroit où vous vous trouvez maintenant.
Ceci vous permettra de voir les objets dans le ciel exactement comme ils apparaissent là où vous êtes présentement.
Le nombre qui apparaît à la droite de cette barre de défilement représente la longitude de l'endroit où se trouve l'observateur.
Latitude
Encore une fois, déplacez le curseur de défilement près de votre latitude approximative sur la Terre. La Terre s’inclinera lorsque vous l’utiliserez.
Si vous vous « déplacez » vers des endroits comme l’hémisphère Sud, l’équateur ou les pôles Nord ou Sud,
vous verrez comment les mouvements quotidiens des étoiles à travers le ciel sont TRÈS différents de ce que vous avez l’habitude de voir dans votre propre ciel!
Vitesse du ciel
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes.
Elle vous permet de déplacer les objets dans les diagrammes à des vitesses variables. Cliquez et maintenez le curseur enfoncé.
Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement.
Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Vous serez quand même en mesure de voir les étoiles circumpolaires du Nord et du Sud en vous plaçant correctement. Vous ne pouvez pas changer où les étoiles sont dans le ciel, mais vous pouvez vous visualiser vous-même à différentes latitudes sur la Terre!
Cette barre de défilement contrôle le temps sidéral, et déplace les étoiles et la grille AD/dec dans le ciel.
Temps sidéral
Utilisez cette barre de défilement pour simuler les mouvements du Soleil à travers le ciel pendant une journée.
Le temps indiqué est connu comme étant le temps « sidéral », et nous devons vous expliquer en quoi ça consiste :
Premièrement, une définition : on dit qu’on objet « culmine » quand il rejoint son point le plus élevé possible dans le ciel. Ceci correspond habituellement au moment où il touche la ligne imaginaire qui part du Nord, puis qui passe à travers le point le plus élevé dans le ciel (appelé le « zénith ») et qui rejoint finalement le point le plus au Sud. Pour les objets circumpolaires, ils peuvent toucher cette ligne deux fois pendant une journée. On parle alors de leur point culminant comme étant le moment où ils touchent cette ligne imaginaire Nord-Sud au-dessus du pôle. Pour des raisons pratiques, pensez à l’endroit où est le Soleil quand il est midi, à l’heure solaire. C’est le moment où le Soleil sera le plus haut dans le ciel de toute la journée. Il ne sera jamais plus haut que ça.
À cause du mouvement de la Terre autour du Soleil, cela prend juste un peu plus de temps à chaque jour pour que le Soleil rejoigne son point culminant que ça en prend pour que les étoiles fassent la même chose. Combien de temps? Un tout petit peu moins que quatre minutes. Cela ne semble pas beaucoup, mais tout cela s’additionne. Sur toute une année, toutes ces minutes additionnées représentent 24 heures complètes!
Il y a très longtemps, les gens utilisaient le Soleil pour dire l’heure. Cela nous donnait une journée « solaire », et c’est sur quoi notre système d’heures est habituellement basé. Mais en astronomie, on aime considérer le temps comme étant relié aux étoiles, et cela veut dire qu’on doit tenir compte de ces quatre minutes de différence. On fait cela en établissant un système de temps qui est basé sur les étoiles plutôt que sur le Soleil, et c’est ce système qu’on appelle « temps sidéral ».
Vous ne pourrez pas trouver d’horloges qui utilisent le temps sidéral dans un magasin près de chez vous (par contre, vous pourriez en trouver en ligne, et il y a plusieurs applications qui peuvent afficher une horloge sidérale sur votre appareil mobile). Mais il y a un endroit où vous pouvez toujours regarder pour savoir quelle heure il est en temps sidéral : les étoiles!
Les astronomes ont établi une méthode pour savoir quelle heure il est présentement en temps sidéral. Il suffit de prendre en note quelle étoile est en train de culminer maintenant (donc, une étoile qui est exactement en direction du Sud dans l’hémisphère Nord, ou exactement en direction du Nord dans l’hémisphère Sud). Puis, trouvez quelle est son AD, et ce sera alors l’heure sidérale actuelle!
On peut prendre l’étoile Antarès comme exemple. Dans le diagramme, placez votre latitude dans l’hémisphère Nord (30°N, par exemple), puis faites une rotation du diagramme pour vous placer au-dessus du pôle Nord de la Terre. L’axe noir qui traverse la Terre sur le diagramme devrait être droit de haut en bas sur l’écran. Maintenant, placez le curseur de défilement du « temps sidéral » à 16h30. Remarquez comment l’étoile Antarès est exactement en plein Sud. L’AD d’Antares est 16h30 (dans environ 35 secondes d’arc!), donc Antarès va rejoindre cet emplacement exact dans le ciel chaque jour à 16h30, heure sidérale – comme une horloge. Vous pourriez même régler votre montre à 16h30 – SI on vivait dans un monde où tous utilisent le temps sidéral!
Par contre, cela ne pourrait presque jamais survenir exactement à 16h30 à votre heure locale, à cause des quatre minutes de décalage qui surviennent à chaque jour entre l’heure solaire et l’heure sidérale. Ces deux heures arriveront au même moment (à plus ou moins une journée d’écart) seulement le 23 septembre de chaque année. D’autres heures sidérales correspondront à leur équivalent solaire à d’autres jours de l’année. On en apprendra plus à propos de ça (et bien d’autres choses) dans le prochain diagramme. Vous pouvez aussi vous rendre au diagramme 15 pour en apprendre plus sur les différences entre un jour solaire et un jour sidéral.
Ce que vous pouvez apprendre :
- Vous pouvez obtenir une introduction simple au temps sidéral.
- Vous pouvez voir comment chaque étoile a une AD définie, et comment cette AD correspond à l’heure sidérale de la culmination de cette étoile.
- Vous pouvez apprendre comment les distances entre les objets dans le ciel sont mesurées en degrés.
À propos du temps sidéral
On va vous expliquer la relation entre le temps sidéral, le temps solaire et le moment de l’année.
Consultez les instructions du diagramme 5Refermer les instructions
Diagramme 5 :
Plus à propos du temps sidéral
Ce que vous pouvez observer :
Le diagramme 5 est semblable au diagramme 4. On a juste ajouté quelques contrôles de plus.
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Montrer l’observateur
Si vous cochez cette case, vous verrez un observateur, un petit bonhomme vert, se tenir sur le dessus de la Terre.
L’horizon qu’on a tracé avec le disque gris et le cercle bleu représentent l’horizon que cet observateur pourrait voir. Décochez la case pour cacher l’observateur.
Réinitialiser l’horizon
Il n’est pas toujours facile d’obtenir exactement la vue que vous voulez. Utilisez ce bouton pour réinitialiser le diagramme.
Tourner la terre
Vous pouvez tourner la Terre pour placer l’observateur exactement à l’endroit où vous vous trouvez maintenant. Ceci vous permettra de voir les objets dans le ciel exactement comme ils apparaissent là où vous êtes présentement.
Le nombre qui apparaît à la droite de cette barre de défilement représente la longitude de l’endroit où se trouve l’observateur.
Latitude
Encore une fois, déplacez le curseur de défilement près de votre latitude approximative sur la Terre. La Terre s’inclinera lorsque vous l’utiliserez.
Si vous vous « déplacez » vers des endroits comme l’hémisphère Sud, l’équateur ou les pôles Nord ou Sud, vous verrez comment les mouvements quotidiens des
étoiles à travers le ciel sont TRÈS différents de ce que vous avez l’habitude de voir dans votre propre ciel!
Vitesse de l’heure locale
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes.
Elle vous permet de déplacer les objets dans les diagrammes à des vitesses variables. Cliquez et maintenez le curseur enfoncé.
Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement.
Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Cette barre de défilement contrôle l’heure locale, et déplace les étoiles et la grille AD/Dec à travers le ciel.
Heure locale
Cette barre de défilement contrôle l’heure solaire approximative « au sommet » de la Terre dans le milieu du diagramme.
« Au sommet » veut dire l’endroit sur la Terre qui est le plus éloigné du cercle gris qui représente l’horizon.
Vitesse du jour de l’année
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes.
Elle vous permet de déplacer les objets dans les diagrammes à des vitesses variables. Cliquez et maintenez le curseur enfoncé.
Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement.
Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Cette barre de défilement contrôle le jour de l’année, et déplace les étoiles et la grille AD/dec à travers le ciel.
Jour de l’année
Déplacez ce curseur de défilement pour changer le jour de l’année.
Note importante à propos des barres de défilement pour le diagramme 5
Lorsque vous allez changer l’heure locale ou le jour de l’année, le ciel au complet va tourner.
La barre pour le temps sidéral en bas va vous montrer l’heure locale sidérale à l’endroit sur la Terre où vous vous situez.
Ceci vous permet de voir comment différentes étoiles peuvent culminer à différentes heures d’une journée solaire, avec leur équivalent en temps sidéral.
Encore une fois, nous allons utiliser Antarès comme exemple. Placez la date au 1er janvier. Déplacez le curseur de défilement pour l’heure locale à 10h15. Le curseur pour le temps sidéral va alors indiquer 16h30. Vous allez voir qu’à ce moment, Antarès est en train de culminer – au beau milieu de la journée! Si vous sélectionnez la date du 30 juillet, alors Antarès va culminer à 20h15.
En utilisant la date du 1er juin, alors Antarès va atteindre son point culminant à minuit. On dit que le 1er juin est la date de la « culmination à minuit » d'Antarès. Chacune des étoiles a une date à laquelle elle culmine à minuit, et il est possible de trouver cette date. Il est intéressant de connaître la date à laquelle un objet culmine à minuit, car ensuite vous pourrez savoir à quel jour de l’année cet objet est le plus haut dans le ciel à minuit. Si vous faites de l’observation avant cette date, alors cette étoile culminera après minuit. Si vous faites de l’observation après cette date, l’étoile culminera avant minuit. Ceci pourra vous aider à planifier vos activités d’observation (et votre horaire de sommeil!) pour la partie de la nuit qui vous convient le mieux.
(Combien de temps avant ou après minuit un objet culminera-t-il? À peu près deux heures pour chaque mois avant ou après la date où l’objet culmine à minuit. Après tout, 360° autour du ciel en 12 mois représente 30° par mois, ce qui est le même que deux heures d’AD!)
Temps sidéral
Cette barre de défilement montre l’heure sidérale pour le même endroit sur la Terre où votre petit observateur vert est situé.
Comme on l’a déjà expliqué, vous ne serez pas en mesure de déplacer le curseur dans cette barre de défilement.
Celui-ci est relié aux valeurs indiquées dans les autres barres.
Ce que vous pouvez apprendre :
- Vous pouvez voir la relation entre l’heure locale solaire, l’heure locale sidérale et le jour de l’année.
- Vous pouvez voir ce que cela veut dire quand on parle de la date où un objet culmine à minuit.
- Vous pouvez voir comment utiliser l’AD de n’importe quel objet céleste, ainsi qu’une application d’horloge sidérale, pour apprendre quand un objet sera à son point le plus haut dans le ciel.
- Vous pouvez voir comme rien de ceci ne dépend de votre latitude, ou même de l’hémisphère dans lequel vous vous trouvez! Lorsque des objets célestes culminent, ils sont à ce moment à leur point le plus élevé dans le ciel possible. Jamais ils ne seront plus hauts que ça. Encore mieux, ils fournissent un mécanisme de surveillance du temps qui ne vous fera jamais défaut – OU qui ne manquera jamais de batterie!
Constellations de l’écliptique (zodiaque)
On va vous donner ici une explication de ce qu’est
l’« écliptique » - la trajectoire imaginaire que suit le Soleil à travers le ciel pendant le cours d’une année.
Consultez les instructions du diagramme 6Refermer les instructions
Diagramme 6 :
Constellations de l’écliptique (zodiaque)
Ce que vous regardez :
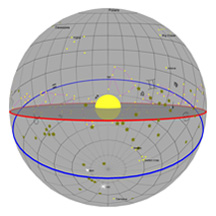
On a placé le Soleil au centre du diagramme cette fois, et il y a une petite planète Terre en orbite autour. C’est réellement comme ça dans la vraie vie!
Le cercle bleu est encore une fois l’équateur céleste.
La plaque grise ronde et plate au centre de la sphère est ce qu’on appelle le plan orbital de la Terre. Pendant la durée d’une vie humaine, cela ne change pas beaucoup d’une année à l’autre. (Par contre, ce n’est pas tout à fait vrai si on considère ce qui se passe pendant plusieurs milliers d’années! Voir le diagramme 7 pour plus d’explications!)
Le cercle rouge est la trajectoire apparente du Soleil à travers le ciel pendant le cours d’une année – appelée l’ « écliptique ». Vous pouvez remarquer que les cercles rouge et bleu sont inclinés un par rapport à l’autre à un angle d’environ 23,5°. C’est l’angle d’inclinaison de l’axe de la Terre.
Vous pouvez aussi remarquer que les cercles rouge et bleu se croisent à deux endroits : dans les constellations des Poissons et de la Vierge. (Vous allez peut-être devoir rechercher quelles sont les constellations qui correspondent aux symboles que nous avons utilisés si vous n’êtes pas familiers avec les figures formées par ces constellations).
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Réinitialiser l’orbite
Ce bouton sert à remettre le cercle rouge (le plan orbital de la Terre) à niveau.
Réinitialiser l’équateur
Ce bouton sert à remettre le cercle bleu (l'équateur céleste) à niveau.
Vitesse du jour de l’année
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes. Elle vous permet de déplacer les objets dans les diagrammes à des vitesses variables.
Cliquez et maintenez le curseur enfoncé.
Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement. Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Cette barre de défilement contrôle le jour de l’année, et déplace la Terre autour du Soleil.
Jour de l’année
Il y a en fait un seul contrôle qu’on peut utiliser ici – mais il est VRAIMENT important! Utilisez cette barre de défilement pour déterminer le jour de l’année,
puis si vous regardez le long de la ligne qui relie la Terre au Soleil, vous pourrez voir dans quelle constellation le Soleil semble se trouver pour cette date.
Vous ne pourrez pas voir d’étoiles dans cette constellation dans le vrai ciel, car le Soleil est tellement brillant qu’il crée ce qu’on appelle le « jour »!
Il y a beaucoup d’aspects à couvrir ici, alors prenons le temps de les aborder un à la fois. En premier, vous pourrez voir que le premier réglage disponible pour le « jour de l’année », celui le plus à gauche, est celui du 21 mars. Ceci correspond à la première journée du printemps dans l’hémisphère Nord. Il y a une raison pour laquelle nous avons choisi cette journée : si vous regardez la ligne qui relie la Terre au Soleil, vous verrez que le Soleil apparaît dans le ciel à un des points où l’écliptique rencontre l’équateur. Ce point-là est très important, car on devait choisir une date avec laquelle « débuter » l’année astronomique. À ce moment-là, la déclinaison du Soleil est de 0°. C’est donc une bonne date pour débuter cette année astronomique. Mais pourquoi donc?
Si vous déplacez le curseur à un jour ou deux après le 21 mars, vous verrez que la déclinaison du Soleil se déplace vers le haut à travers les étoiles. Cela veut dire qu’il devient plus haut dans le ciel, et que l’été approche. Le premier jour du printemps (aussi appelé « équinoxe vernal ») semble très bien convenir pour débuter notre année astronomique. En passant, l’expression « équinoxe vernal » a deux origines différentes - « vernal » vient de « ver », ce qui veut dire « printemps » en latin – et « équinoxe » veut dire « égal à la nuit ». Rappelez-vous, dans le diagramme 1, on pouvait voir que le Soleil se levait à 6h et se couchait à 18h – donc le jour et la nuit sont de la même longueur. (Ceci survient aussi lors du premier jour d’automne, appelé « équinoxe d’automne ».)
Les astronomes ont été un peu plus loin avec ce point représentant l’équinoxe vernal. Rappelez-vous comment l’AD est l’équivalent de la « longitude » dans le ciel? Et bien, sur la Terre, on a dû décider quel point en particulier utiliser pour la ligne de la longitude 0°. Les astronomes se sont tout simplement entendus pour utiliser l’Observatoire de Greenwich au Royaume-Uni, alors c’est l’endroit qu’on utilise pour débuter la mesure de la longitude sur la Terre. On a besoin d’un point similaire dans le ciel, pour définir la marque 0h pour l’AD, et vous l’aurez deviné – c’est le point de l’équinoxe vernal qui a été choisi.
Les astronomes désignent aussi ce point comme étant le « premier point du Bélier », même si ce point est situé dans la constellation des Poissons! Mais il y a longtemps (quelques milliers d’années), alors que les astronomes de la Grèce antique étudiaient toutes ces choses, ce point était en effet situé dans la constellation du Bélier. Il s’est déplacé depuis (!) à cause d’un effet appelé « précession », ce qui est un peu en-dehors de la portée de ce diagramme (nous y reviendrons au diagramme 11!). La précession amène l’orbite entière de la Terre à se déplacer comme une toupie qui oscille alors qu’elle ralentit. Cet effet de précession amène toute l’écliptique à effectuer une rotation très lentement dans l’espace. Vous pourrez en apprendre plus dans les diagrammes 11 et 12, car il y a vraiment des choses intéressantes qui se passent à cause de la précession : par exemple, l’été dans l’hémisphère Nord aura lieu en décembre dans 12 000 ans, et Polaris ne sera plus notre étoile polaire d’ici quelques milliers d’année. (N’oubliez pas que les pyramides d’Égypte qui sont parfaitement alignées avec le « vrai Nord » - du moins, avec l’endroit où il était situé il y a 5 000 ans!)
Si vous êtes familiers avec l’astrologie, vous savez que le Bélier est aussi le premier signe du zodiaque – un peu comme le concept du « premier point du Bélier » en astronomie. Le Soleil se situe toutefois aujourd’hui dans la constellation des Poissons pendant les dates astrologiques traditionnelles du « Bélier », et ce décalage survient exactement pour la même raison – la précession qui a eu lieu depuis que les définitions astrologiques ont été mises en place il y a tant de siècles.
De retour dans le présent : vous pourrez remarquer qu’à certains moments de l’année, le Soleil a une déclinaison plus élevée, ce qui veut dire que le Soleil est plus haut dans le ciel dans l’hémisphère Nord, alors que les rayons du Soleil sont beaucoup plus perpendiculaires au sol à ce moment-là. Sans faire trop de mathématiques, c’est pourquoi l’été dans l’hémisphère Nord survient pendant ces mois-là. Un phénomène similaire survient dans l’hémisphère Nord pendant les mois d’hiver : à ce moment-là, la déclinaison du Soleil est négative, alors sa position est plus élevée dans le ciel pour les gens de l’hémisphère Sud – ce qui leur donne décembre et janvier comme mois d’été.
Puisque les changements dans la déclinaison du Soleil sont causés par l’angle entre l’équateur céleste et le plan de l’écliptique, et que cela est causé par l’inclinaison de l’axe de rotation de la Terre, alors on peut affirmer de façon certaine qu’on a des saisons à cause de l’inclinaison de la Terre! Les changements de saisons n’ont rien à voir avec le fait que la Terre est proche ou loin du Soleil; en fait, l’été de l’hémisphère Nord survient à un moment de l’année où la Terre est en réalité un peu plus loin du Soleil qu’elle ne l’est en hiver! TCe double coup dur fait que les gens de l’hémisphère Sud vivent un été un peu plus chaud que dans le Nord. Le fait qu’il y a une plus grande superficie recouverte par les eaux dans l’hémisphère Sud aide un peu à compenser, mais ceci sort des limites de l’astronomie!
Pendant le cours d’une année, le Soleil semble se déplacer à travers 12 constellations. Elles sont connues comme étant les constellations du zodiaque. Le mot « zodiaque » vient de la même racine que « zoo », ce qui veut dire « animal ». Seules 7 des 12 constellations représentent des animaux, mais cela semble représenter une proportion suffisamment élevée pour en justifier le nom.
Pendant que nous y sommes, on a aussi inclus des constellations qui ont été historiquement ignorées, comme Ophiuchus. Il y a une période d’environ 18 jours au début décembre où le Soleil semble se trouver à l’intérieur des limites d’Ophiuchus. Apparemment, lorsque des hommes s’asseyaient ensemble il y a très longtemps pour tenter de comprendre tous ces phénomènes, le fait qu’Ophiuchus nous aurait donné 13 signes du zodiaque pour seulement 12 mois a pesé plus lourd dans la balance que le fait que la constellation par elle-même représente un monsieur qui tient un serpent, ce qui aurait entré dans la thématique zoologique. Malheureusement, cette exclusion veut dire que vous ne trouverez pas d’horoscope aujourd’hui pour les personnes nées sous le « signe d’Ophiuchus » - par contre, si votre anniversaire tombe dans la première moitié de décembre, vous savez maintenant pourquoi tout ce qui concerne les Sagittaires ne semble pas toujours vous correspondre!
Ce que vous pouvez apprendre :
- Vous pouvez voir dans quelle constellation le Soleil apparaît pour n’importe quel jour de l’année.
- Vous pouvez comment le « zodiaque » est fait, et comment il est lié à l’expression astronomique « écliptique ».
- Vous pouvez voir comment le Soleil change sa déclinaison pendant le cours de l’année, ce qui cause les saisons.
- Vous pouvez voir pourquoi certaines étoiles ne sont pas visibles dans le ciel pendant certains moments de l’année – parce qu’elles sont trop près du Soleil!
L’écliptique (vue centrée sur la Terre)
On a redessiné le diagramme 6 pour vous montrer plus clairement la trajectoire du Soleil à travers le zodiaque.
Consultez les instructions du diagramme 7Refermer les instructions
Diagramme 7:
L’écliptique (vue centrée sur la Terre)
Ce que vous regardez :
À la base, c’est le même diagramme que le diagramme 6; on a juste placé la Terre au centre, et placé le Soleil dans le ciel de la même manière qu’il apparaît depuis la Terre. Le zodiaque, l’écliptique et l’équateur sont les mêmes que précédemment.
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Réinitialiser l’orbite
Ce bouton sert à remettre le cercle rouge (le plan orbital de la Terre) à niveau.
Réinitialiser l’équateur
Ce bouton sert à remettre le cercle bleu (l'équateur céleste) à niveau.
Tourner la terre
On vous fournit cette commande car il est bien de pouvoir voir comment le Soleil éclaire la Terre à différents moments de la journée. Il n’y a pas vraiment rien de plus à ajouter à ça.
Jour de l’année
Cette barre de défilement fait la même chose que ce qu’elle faisait dans le diagramme 6, mais maintenant, avec le Soleil qui se « déplace » à travers les constellations,
il est beaucoup plus facile de voir où le Soleil se situe dans le ciel.
Même si on sait qu’une vue centrée sur la Terre n’est pas astronomiquement exact, ça aide quand même de pouvoir l’imaginer de cette façon – parce que cela reflète ce qu’on voit réellement depuis la Terre!
Vitesse du jour de l’année
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes. Elle vous permet de déplacer les objets dans les diagrammes à des vitesses variables.
Cliquez et maintenez le curseur enfoncé.
Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement. Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Cette barre de défilement contrôle le jour de l’année, et déplace le Soleil à travers l’écliptique tout en faisant tourner la Terre.
Ce que vous pouvez apprendre :
- À la base, les mêmes choses que ce que vous pouviez voir dans le diagramme 6… mais plus facile à visualiser!
- Ne vous laissez pas méprendre par la simplicité – ce « mouvement » annuel apparent du Soleil à travers le zodiaque est un concept astronomique TRÈS important.
Introduction aux éclipses
Un diagramme très simple pour vous montrer comment les mouvements de la Lune
autour de la Terre peuvent mener à des éclipses solaires et lunaires.
Consultez les instructions du diagramme 8Refermer les instructions
Diagramme 8 :
Introduction aux éclipses
Ce que vous regardez :
On a aplati l’orbite de la Lune autour de la Terre, et le cercle gris pour l’horizon au centre de la sphère est parallèle à cette orbite. Vous pouvez faire monter et descendre la Lune avec la barre de défilement pour la déclinaison, et vous pouvez faire bouger la Lune autour de la Terre. (La direction du Soleil est fixe.)
On a aussi ajouté une vue en médaillon de la Lune comme elle est vue depuis la Terre. Vous pouvez alors voir les différentes phases de la Lune changer alors qu’elle se déplace dans la trajectoire de son orbite mensuelle.
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Réinitialiser l’horizon
Il n’est pas toujours facile d’obtenir exactement la vue que vous voulez. Utilisez ce bouton pour réinitialiser l’horizon.
Déclinaison
Déplacez le curseur pour faire bouger la Lune de haut en bas. Alors que la Lune se déplace autour de la Terre à chaque mois, sa déclinaison change.
Ici, on a tellement simplifié les choses que l’utilité réelle de cette commande est de pouvoir déplacer la Lune suffisamment loin vers le haut ou vers le bas pour pouvoir entrer ou sortir d’une situation d’éclipse.
Si vous déplacez la Lune vers une déclinaison de 0°, alors vous pourrez voir son ombre sur la Terre lors de la nouvelle lune, et l’ombre de la Terre sur elle à la pleine lune –
pareil comme quand de véritables éclipses surviennent! Veuillez noter qu'on a réglé la déclinaison du Soleil à 0° pour ce diagramme; la Lune est la seule chose qui bouge!
Dans le prochain diagramme, nous allons vous montrer comme la déclinaison de la Lune change aussi quand elle se déplace autour de la Terre.
Bien sûr, les éclipses n’arrivent pas aussi souvent que ce que ce diagramme pourrait vous faire croire. Nous allons vous en dire plus sur cela dans le prochain diagramme, mais pour maintenant, remarquez comment la position de la Lune dans son orbite peut ou bien prévenir, ou bien causer des éclipses. La déclinaison de Lune au moment où elle pourrait causer une éclipse – ou être elle-même éclipsée – est extrêmement critique!
Jour du mois
Déplacez le curseur pour déplacer la Lune autour de la Terre et voir les phases.
Vitesse du jour du mois
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes. Elle vous permet de déplacer les objets dans les diagrammes à des vitesses variables.
Cliquez et maintenez le curseur enfoncé.
Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement. Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Cette barre de défilement contrôle le jour du mois.
Tourner la terre
Encore une fois, vous pouvez faire une rotation de la Terre pour simuler le Soleil qui en éclaire différentes parties au fur et à mesure que la journée avance.
Ce que vous pouvez apprendre:
- Vous pouvez voir ce qui cause les phases de la Lune.
- Vous pouvez voir un modèle très simple qui explique pourquoi les éclipses surviennent.
Les trajectoires du Soleil et de la Lune à travers le zodiaque
Une vue plus réaliste des mouvements de la Lune et du Soleil -
pour vous en montrer encore plus à propos des éclipses!
Consultez les instructions du diagramme 9Refermer les instructions
Diagramme 9 :
Les trajectoires du Soleil et de la Lune à travers le zodiaque
Ce que vous regardez :
Maintenant, les choses commencent à devenir intéressantes! Les constellations sont de retour (mais pour que ce soit plus clair, on a retiré les étoiles pour l’instant), et on a placé les orbites du Soleil (cercle rouge) et de la Lune (cercle vert) par-dessus. Tout est centré autour de la Terre et, encore une fois, le cercle bleu est l’équateur céleste.
La trajectoire rouge du Soleil est appelée l’ «écliptique ». Elle est inclinée de 23,4° par rapport à l’équateur de la Terre à cause de l’inclinaison de l’axe de la Terre. C’est plus précis ici que dans les diagrammes précédents. Maintenant, nous avons besoin de cette précision supplémentaire.
On a ajouté la trajectoire orbitale de la Lune en vert, qui est inclinée de 5,1° par rapport à l’écliptique. Ceci rend le tout aussi précis qu’on peut le montrer dans un diagramme comme celui-ci. Nous avons choisi le premier point du Bélier pour avoir ces deux orbites qui se croisent, mais en réalité, ce point d’intersection change graduellement avec le temps (plus à propos de ça plus tard!)
Il y a un nouveau symbole qu’on a placé au premier point du Bélier. Lorsque le diagramme se charge, à ce point-là, le Soleil et la Lune sont à la même déclinaison (0°), et leurs trajectoires se croisent. Au fur et à mesure que le temps avance, la Lune se déplace au-dessus de l’écliptique. Deux semaines plus tard, de l’autre côté du ciel, vous verrez que les orbites se croisent de nouveau – et cette fois, alors qu’on avance dans le temps, la Lune se déplace en-dessous de l’écliptique. Nous allons nommer ces deux points dans l’orbite de la Lune comme étant respectivement le “nœud ascendant” et le “nœud descendant”.
On dit « nœud », car les deux orbites se croisent, et que c’est le nom traditionnellement donné aux points importants dans toutes sortes de différentes cartes de réseaux. On dit aussi « ascendant » et « descendant », car la Lune se déplace « en haut », au-dessus de l’écliptique, ou « en bas », en-dessous de l’écliptique, à ces deux points respectifs. Un petit symbole ressemblant à un fer à cheval avec des cercles à ses extrémités se trouve à chacun des nœuds. Il a son ouverture vers le bas au nœud ascendant, et vers le haut au nœud descendant.
Mouvements des nœuds
Ces nœuds se déplacent! C’est vrai, les astronomes ont déterminé il y a longtemps que la « ligne des noeuds » (la ligne imaginaire qui traverse la Terre et qui connecte les deux nœuds) se déplace très lentement,
dans la direction opposée à laquelle le Soleil et la Lune semblent se déplacer à travers le ciel. Alors, pendant que la Lune prend un mois à tourner autour de la Terre,
et que le Soleil prend une année, chacun des nœuds prend 18,6 années pour effectuer une orbite! Ceci est un point très important quand vient le temps de prédire des éclipses.
Vous avez maintenant accès à des contrôles qui permettent de bouger tout ce que vous voyez. Vous pouvez faire faire une rotation à la Terre, vous pouvez déplacer la Lune et le Soleil, vous pouvez même faire tourner les nœuds. Ceci vous permet de visualiser ce qui se passe avec chaque pièce du casse-tête que les éclipses représentent. Il faut par contre garder à l’esprit que l’échelle de temps pour chacun de ces mouvements est très différente!
Il faut aussi se rappeler qu’on a placé les nœuds et la Lune à des endroits plutôt aléatoires. Le « jour de l’année » s’applique seulement au Soleil, car il est possible que les nœuds et la Lune puissent se retrouver à n’importe quel endroit de leurs orbites respectives pour une journée donnée. Le Soleil, par contre, sera toujours au même endroit dans le ciel pour la date qui est affichée.
On a aussi représenté la Lune et le Soleil comme étant un petit peu plus gros qu’ils ne le sont réellement dans le véritable ciel. Les tailles choisies pour les représenter sont un compromis entre utiliser leur véritable taille à l’échelle (vous auriez de la difficulté à les voir!) ou choisir une taille trop grande (ce qui nous empêcherait de vous montrer quoi que ce soit de réaliste sur comment les éclipses surviennent). Ceci est un outil éducatif, non pas un ordinateur servant à prédire de manière rigoureuse les mécaniques célestes!
Ce que vous devez remarquer dans ce diagramme, c’est comment la Lune, le Soleil et les nœuds doivent être alignés quasiment parfaitement pour que n’importe quelle sorte d’éclipse puisse survenir. Pour une éclipse solaire, le Soleil et la Lune doivent se retrouver au même endroit dans le ciel en même temps. Mais même si cela arrive, si les deux ne se retrouvent pas à un nœud, alors la Lune va se retrouver « au-dessus » ou « en-dessous » du Soleil, et alors, il n’y aura pas d’éclipse! En fait, c’est ce qui arrive la plupart du temps quand la Lune et le Soleil ont la même AD.
Mais à des moments très particuliers, quand le Soleil et la Lune sont au même endroit dans le ciel au même moment, ET qu’ils se retrouvent à un nœud, alors on a une éclipse! Essayez de reproduire ces circonstances, et vous pourrez voir l’ombre de la Lune sur la Terre!
Si vous placez le Soleil à un nœud, et la Lune au nœud opposé alors vous aurez droit à une éclipse lunaire – comme ce serait le cas dans le vrai ciel.
Vous pourriez être tenté de croire que vous pouvez « aligner » la Terre, la Lune et le Soleil pour qu’une éclipse lunaire ou solaire survienne lorsque le Soleil et la Lune sont ailleurs qu’à un nœud. Ça semble tentant, mais l’échelle de ce diagramme ne permet pas de montrer les véritables distances observées dans le vrai univers. Si le Soleil est haut dans son orbite, et que la Lune est basse dans son orbite, alors la « ligne » entre le Soleil et la Lune ne croisera pas du tout la Terre. Désolé que ce diagramme ne montre pas cette situation aussi clairement qu’on le souhaiterait, mais c’est comme ça que ça fonctionne dans la vraie vie!
Tailles relatives
On vous a aussi fourni une commande qui permet de changer la taille relative de la Lune par rapport au Soleil. On ne peut pas montrer ceci dans le diagramme, mais les orbites de la Lune autour de la Terre,
et de la Terre autour du Soleil, ne sont pas des cercles parfaits. Ce que ça veut dire, c’est que la Lune et le Soleil semblent parfois un peu plus gros ou un peu plus petits qu’ils ne le sont à d’autres moments.
À cause de ça, parfois la Lune semble juste un peu plus petite que le Soleil, et parfois un peu plus grosse.
Vous ne remarquerez jamais ceci, à moins d’être un astronome avec des instruments de mesure, OU… pendant une éclipse solaire!
S’il y a une éclipse solaire, et si la Lune est un petit peu plus grosse que le Soleil, alors on va avoir une éclipse totale. Si la Lune est un peu plus petite que le Soleil, alors on aura ce qu’on appelle une éclipse annulaire (en forme d’anneau). Dans ce cas, la Lune ne sera pas en mesure de recouvrir le Soleil complètement, et il y aura un anneau de Soleil autour de la Lune. L’éclipse ne sera pas totale.
Cette commande qu’on vous a fournie vous permet de régler la taille relative de la Lune par rapport au Soleil, pour que vous puissiez y aller du plus petit au plus grand ratio possible. Ceci vous permettra de simuler une éclipse annulaire ou encore une éclipse totale.
Il est même possible de s’arranger pour que la Lune et le Soleil semblent avoir quasiment la même taille. La Lune recouvre alors à peine le Soleil pendant le milieu de l’éclipse, mais ne le recouvre pas complètement au début et à la fin de l’éclipse. C’est parce que la surface de la Terre s’éloigne de la Lune. Aux moments du lever et du coucher du soleil, l’endroit d’où on observe sur la Terre est juste assez loin de la Lune pour que l’éclipse soit annulaire à ces moments-là! Ce genre d’éclipse est assez rare, mais est suffisamment fréquente pour que plusieurs personnes les appellent éclipses « hybrides ». La plupart des astronomes préfèrent le nom « annulaire-totale », puisque c’est ce qui se passe quand l’ombre de la Lune traverse la surface de la Terre.
On vous mentionne ceci, parce que l’éclipse du 20 avril 2023 sera une éclipse de ce type. La plupart des gens observeront la phase totale de cette éclipse depuis l’Indonésie et depuis une petite région dans l’extrême ouest de l’Australie.
Comme vous pouvez le voir, les mouvements réels de la Terre, de la Lune et du Soleil sont très complexes. Orbites elliptiques, nœuds qui révolutionnent lentement… Pour ce qui est des prédictions d’éclipses, nous ne faisons qu’effleurer la surface ici! Mais nous espérons que ceci vous aide à avoir une meilleure compréhension des précautions que nous devons prendre pour être en mesure de faire tous ces calculs.
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Réinitialiser l’équateur
Utilisez ce bouton pour remettre à niveau l’équateur de la Terre.
Taille relative
Cette commande vous permet de modifier la taille relative de la Lune par rapport au Soleil et de simuler ce qu’on observe dans la vraie vie dans le ciel!
Vitesse du temps
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes. Elle vous permet de déplacer les objets dans les diagrammes à des vitesses variables.
Cliquez et maintenez le curseur enfoncé.
Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement. Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Cette barre de défilement contrôle les mouvements de la Lune, du Soleil et de la Terre dans le diagramme.
Tourner la terre
Vous permet d’effectuer une rotation de la Terre, comme avant. Cette fois, si vous simulez une éclipse solaire, vous pourrez voir la Terre effectuer sa rotation en-dessous de l’ombre de la Lune!
(Mais s’il-vous-plaît, attendez au prochain diagramme avant de nous dire que l’éclipse devrait se déplacer de l’Est vers l’Ouest au-dessus de la Terre!)
Jour du mois
Cette barre de défilement déplace la Lune autour de la Terre pendant la durée complète d’un mois hypothétique. Aucune journée en particulier n’est représentée ici;
c’est seulement pour vous montrer les mouvements relatifs de la Lune par rapport au Soleil et aux nœuds.
Jour de l’année
Cette barre de défilement déplace le Soleil dans sa trajectoire à travers l’écliptique pour une année hypothétique complète.
Encore une fois, aucune année précise n’est représentée ici, mais la date indiquée est suffisamment précise pour bien indiquer où le Soleil se trouve dans le ciel ce jour-là pendant une année donnée.
Ce que vous pouvez apprendre :
- Vous pouvez voir ce qui cause les éclipses, et pourquoi elles surviennent seulement quand la Lune et le Soleil sont très près des nœuds de leur trajectoires respectives à travers le ciel.
- Vous pouvez vous faire une idée de l’importance des mouvements de ces objets dans le ciel au fil du temps.
- Vous pouvez vous-même simuler des éclipses, incluant les éclipses solaires totales et annulaires.
- Vous pouvez apprécier à quel point les relations entre les mouvements des objets célestes sont belles.
- Vous pouvez également apprécier à quel point les anciens scientifiques étaient brillants d’avoir découvert et documenté tout ceci, sans l’aide de télescopes, d’ordinateurs ou même de calculs.
Combiner les mouvements du Soleil, de la Lune et des noeuds
On a tout mis ensemble pour vous, et on vous a donné un outil pour observer les mouvements relatifs de tous les acteurs principaux du grand jeu de l’éclipse!
Consultez les instructions du diagramme 10Refermer les instructions
Diagramme 10 :
Combiner les mouvements du Soleil, de la Lune et des noeuds
Ce que vous regardez :
On a aplati l’orbite de la Lune autour de la Terre, et le cercle gris représentant l’horizon dans le milieu de la sphère est parallèle à cette orbite. Vous pouvez monter et descendre la déclinaison de la Lune et vous pouvez déplacer la Lune autour de la Terre. (La direction du Soleil est fixe.)
On a aussi ajouté une vue en médaillon de la Lune comme elle peut être observée depuis la Terre. Ainsi, vous pouvez voir les phases de la Lune changer alors qu’elle se déplace dans sa trajectoire orbitale mensuelle.
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Réinitialiser l’équateur
Utilisez ce bouton pour remettre à niveau l’équateur de la Terre.
Taille relative
Cette commande vous permet de modifier la taille relative de la Lune par rapport au Soleil et de simuler ce qu’on observe dans la vraie vie dans le ciel!
Vitesse du temps
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes. Elle vous permet de déplacer les objets dans les diagrammes à des vitesses variables.
Cliquez et maintenez le curseur enfoncé.
Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement. Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Cette barre de défilement contrôle les mouvements de la Lune, du Soleil, de la Terre et des nœuds dans le diagramme.
Jour du mois
Utilisez cette barre de défilement pour déplacer la Lune autour de la Terre et en voir les phases. Dans le prochain diagramme, on vous montrera comme la déclinaison de la Lune change alors qu’elle se déplace autour de la Terre.
Jour de l’année
Cette barre de défilement déplace le Soleil dans sa trajectoire à travers l’écliptique pour une année hypothétique complète. Encore une fois, aucune année précise n’est représentée ici,
mais la date indiquée est suffisamment précise pour bien indiquer où le Soleil se trouve dans le ciel ce jour-là pendant une année donnée.
Noeuds
Cette barre de défilement déplace les nœuds. Ceux-ci font une révolution complète à travers le zodiaque en un peu plus de 223 mois. Cela représente 18,6 annéees!
Ça veut aussi dire que les nœuds peuvent se retrouver dans n’importe quelle constellation; c’est pourquoi les éclipses peuvent survenir à n’importe quel moment de l’année.
Remarquez que les nœuds se déplacent dans la direction « opposée » à celle du Soleil et de la Lune.
Tourner la Terre
Encore une fois, vous pouvez effectuer une rotation de la Terre pour simuler comment le Soleil en éclaire différentes parties au fur et à mesure que la journée avance.
Ce que vous pouvez apprendre :
- Vous pouvez voir ce qui cause les phases de la Lune.
- Vous pouvez voir un modèle très simple expliquant pourquoi les éclipses surviennent.
- Vous pouvez apprendre pourquoi les éclipses peuvent survenir n’importe où le long de l’écliptique, à n’importe quel temps de l’année – mais seulement à certains moments bien précis.
Mouvements apparents et réels du Soleil et de la Lune
Ici, vous verrez comment la Lune et le Soleil semblent se déplacer dans le ciel, et comment ils se déplacent réellement!
Consultez les instructions du diagramme 10aRefermer les instructions
Diagramme 10a:
Apparent and Real Motion of the Sun and Moon
Ce que vous regardez :
Ce diagramme est conçu pour répondre à une question que plusieurs personnes ont quand ils commencent à étudier l’astronomie : Si la Lune et le Soleil se lèvent à l’est et se couchent à l’ouest, comment est-ce possible qu’ils se déplacent en fait de l’ouest vers l’est? Et pourquoi les éclipses se déplacent-elles de l’ouest vers l’est?
La réponse facile est que la Terre tourne sur son axe une fois par jour, et pour nous qui tournons avec la Terre, il semble que les choses se déplacent d’est en ouest. Ce diagramme décompose la situation pour vous, afin que vous puissiez facilement voir les vrais mouvements.
Nous avons conservé plusieurs des mêmes caractéristiques que les diagrammes précédents : vous avez les arcs rouges, bleus et verts qui forment l’équateur, l’écliptique et la trajectoire orbitale de la Lune à travers le ciel. La grille AD/Dec et quelques étoiles sont là comme référence, et le Soleil et la Lune sont en place ensemble, prêts à vous montrer leurs mouvements apparents et réels dans le ciel.
Les mouvements de la Lune
La Lune effectue son orbite autour de la Terre une fois par mois. Dépendamment de comment vous voulez configurer la date exacte de début et de fin pour le « mois » (il y a au moins CINQ différents types de mois en astronomie!), la durée exacte d’un mois varie d’un peu plus de 27 jours à environ 29,5 jours (à peu près). Dans ce diagramme, on a utilisé 28 jours pour notre mois parce que c’est un nombre rond, qui représente exactement quatre semaines, et l’idée de base que nous tentons de démontrer ne dépend pas de ça de toute manière.
La Lune effectue son orbite autour de la Terre d’ouest en est. Ça veut dire que si vous vous trouvez au-dessus du pôle Nord de la Terre, la Lune semble se déplacer dans le sens opposé des aiguilles d’une montre. Dit d’une autre manière, si vous faites face au sud dans l’hémisphère nord, les mouvements orbitaux de la Lune la déplacent de la « droite » vers la « gauche » à travers sa trajectoire dans le ciel. Dans l’hémisphère sud, en faisant face au nord, ces mouvements seraient de la « gauche » vers la « droite ».
C’est bien connu que si vous marchez à l’extérieur pour regarder la Lune, et que vous prenez en note sa position dans le ciel, vous pouvez sortir de nouveau quelques heures plus tard et elle semblera avoir bougé dans la direction opposée de ce qu’on a décrit! Qu’est-ce qui se passe?
Il y a deux facteurs en jeu ici : Premièrement, ce mouvement dans la Lune dans son orbite est comparativement très lent. Après tout, la Lune prend un mois complet pour faire tout le tour du ciel une fois! Deuxièmement, la Terre fait une rotation. Le mouvement que vous voyez quand vous regardez la Lune pendant le cours d’une soirée est beaucoup plus rapide. La Lune semble alors se déplacer à l’autre bout du ciel pendant le cours d’une seule nuit! C’est parce que ce mouvement est dû à la rotation de la Terre. À cause de ça, la Lune semble se déplacer d’est en ouest dans le ciel. Vu que la Terre tourne plus vite que la Lune ne se déplace vraiment, ça fait en sorte que la Lune semble se déplacer dans une direction, alors qu’en fait elle se déplace dans l’autre direction.
Si vous êtes dans une voiture, conduisant sur la route, et que vous arrivez près d’une voiture qui se déplace plus lentement que vous, alors si vous étiez en mesure d’effacer toutes les références extérieures (comme les maisons, les arbres, les lignes sur la route, etc), vous auriez l’impression que l’autre voiture se déplacerait de reculons! Elle se déplace réellement vers l’avant, mais parce qu’elle ne se déplace pas aussi vite que vous, vous la dépassez et la laissez en arrière. Dans cette situation, il n’y a pas plus de différence dans la vitesse ou la position relative entre vos deux voitures que si vous étiez assis immobile et que vous dépasseriez la voiture lentement, ou que si vous étiez immobile et que la voiture se déplaçait réellement de reculons! C’est la même chose avec les mouvements de la Lune.
Les mouvements du Soleil
Il y a des similarités et des différences entre les mouvements apparents du Soleil et de la Lune. La Terre tourne de la même manière dans les deux cas, mais le Soleil ne se déplace pas dans une orbite autour de la Terre! La trajectoire du Soleil à travers le zodiaque prend une année entière, et comme on l’a déjà vu, c’est parce que dans ce cas-ci, c’est la Terre qui effectue une révolution. La situation du Soleil n’est pas aussi intuitive que celle de la Lune pour plusieurs raisons : premièrement, il n’y a pas d’étoiles visibles près du Soleil, ce qui aurait permis de juger de ses mouvements à travers le ciel causés par l’orbite de la Terre. Deuxièmement, ce mouvement est très lent. Cela prend une année complète au Soleil pendant que la Lune se déplace autour du ciel à l’intérieur d’un mois! Troisièmement, ce n’est pas vraiment le Soleil qui se déplace – c’est la Terre! On doit prétendre que c’est le Soleil qui bouge parce que c’est ce à quoi ça ressemble pour nous. Et finalement, les mouvements quotidiens du Soleil semblent énormes pour nous (pareil comme pour la Lune), mais c’est parce que la Terre tourne – et nous amène avec elle pour ce tour de manège! Cette combinaison de mouvement lent,
de manque de cadre de référence, du modèle très familier de « se lève à l’est et se couche à l’ouest » nous conditionne à ne pas être en mesure de visualiser ce qui se passe réellement.
Deux scénarios illustrés par le diagramme
Ce diagramme éclaircit quelque peu les choses en séparant ces deux mouvements complètement. Premièrement, vous pouvez faire tourner le Soleil, la Lune et le nœud de la Lune pour les place où vous voulez. Vous pouvez placer le Soleil en haut ou en bas dans le ciel, et en haut ou en bas le long de l’écliptique. Vous pouvez régler la déclinaison de la Lune en haut ou en bas du Soleil. Vous pouvez même utiliser le curseur pour le « mouvement apparent » pour placer le Soleil au-dessus de l’horizon lorsqu’il est dans la partie du zodiaque que vous souhaitez. Rien de cela n’aura d’importance lorsque viendra le temps de vous montrer les mouvements réels et apparents de la Lune et du Soleil, parce ceux-ci ne changent jamais.
Une fois que vous avez tout mis en place comme vous le souhaitez, alors le plaisir commence!
Montrer le mouvement réel
Celui-ci est le plus facile à voir, et il correspond avec ce qu’on vous a montré dans des diagrammes précédents. Vous pouvez utiliser le curseur régulier pour garder les choses en mouvement dans une boucle continue. Vous remarquerez que la Terre tourne elle aussi, parce que depuis le point de vue du système solaire, c’est ce qui se passe réellement.
Remarquez que la Lune se déplace beaucoup plus vite que le Soleil à travers le ciel. À chaque mois, elle rattrape le Soleil et le dépasse. On ne voit jamais ça arriver, car à ces moments-là, c’est la Nouvelle Lune – la face cachée de la Lune est éclairée par le Soleil, et nous ne pouvons pas la voir (sauf pendant une éclipse solaire!).
Montrer le mouvement apparent
Dans cette situation, on arrête la Terre complètement et on déplace le ciel avec tout ce qu’il y a dedans. Si vous utilisez le curseur régulier, vous verrez les mouvements survenir pendant le cours d’un jour, et tout semble se déplacer d’est en ouest, comme vous pourriez vous y attendre. Vous pouvez voir le Soleil, la Lune et les étoiles bouger dans la même direction dans le ciel à laquelle vous êtes habitués.
Mais si vous configurez les choses pour que le Soleil et la Lune soient proches un de l’autre, et que vous les placez près de certaines étoiles pour les utiliser comme des références, alors vous verrez quelque chose d’intéressant. Utilisez le curseur pour la vitesse du mouvement apparent pour exécuter le scénario pendant un jour ou deux, et vous verrez que la Lune s’est déplacée dans son orbite (vers l’est). En relation avec le Soleil, elle semblera s’être déplacée d’une bonne distance même en un seul jour. C’est parce qu’elle a le même mouvement orbital qu’elle avait avant, lorsque vous avez utilisé le curseur pour le mouvement réel. Ce mouvement ne s’est pas arrêté, même si les choses semblent maintenant tourner dans le ciel dans l’autre sens.
En fait, si vous exécutez le curseur pour la vitesse du mouvement apparent pour quelques jours, vous pourrez aussi voir que le Soleil a aussi avancé dans son orbite. Exécutez-le pour une année complète, et le Soleil aura aussi traversé tout le ciel, se déplaçant d’ouest en est, même s’il se lève à chaque jour à l’est et se couche à l’ouest!
Il est intéressant de comparer ce que vous voyez ici avec le vrai ciel. Placez la Lune et le Soleil au même endroit, et exécutez le curseur pour le mouvement apparent pour un jour. Vous verrez que la une s’est déplacée d’environ 15 degrés – une ligne d’AD dans notre grille. C’est une grande distance dans le vrai ciel – environ 30 diamètres de Lune – et c’est beaucoup plus grand que ce qui apparaît ici parce qu’on a représenté la Lune et le Soleil environ 7 fois plus grands dans le ciel qu’ils ne le sont réellement. Mais si vous allez à l’extérieur et regardez l’emplacement de la Lune par rapport à une étoile, puis que vous allez à l’extérieur la nuit suivante et trouvez la même étoile, vous verrez qu’à coup sûr, la Lune se sera déplacée d’une bonne distance vers l’est. Vous voyez alors le résultat de la Lune qui se déplace dans son orbite!
Le mouvement de la Lune dans son orbite peut aussi être observé pendant les éclipses. Plus à propos de ça dans de prochains diagrammes!
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Montrer l’observateur
Si vous cochez cette case, vous verrez un observateur, un petit bonhomme vert, se tenir sur le dessus de la Terre. L’horizon qu’on a tracé avec le disque gris et le cercle bleu représentent l’horizon que cet observateur pourrait voir. Décochez la case pour cacher l’observateur.
Réinitialiser l’horizon
It's not always easy to get the view exactly the way you want it. Use this button to get the horizon level again!
Tourner la Terre
Vous pouvez faire tourner la Terre pour placer l’observateur à l’endroit où vous vous trouvez. Ceci vous montrera les objets dans le ciel exactement comme ils apparaîtraient à l’endroit où vous êtes.
Latitude
Comme dans les diagrammes précédents, ceci vous place à quelque part sur la Terre à une latitude donnée.
Lune
Ce contrôle vous permet de placer la Lune où vous voulez le long de sa trajectoire.
Soleil
Tout comme avec la barre de défilement pour la Lune, vous pouvez utiliser ce contrôle pour placer le Soleil où vous voulez le long de l’écliptique.
Nœuds
Avec ce contrôle, vous pouvez déterminer la position des nœuds ascendants et descendants de l’orbite de la Lune. Vous pouvez l’utiliser après avoir déterminé les positions de la Lune et du Soleil dans leurs orbites, pour amener la déclinaison de la Lune à être au-dessus, en-dessous ou égale à celle du Soleil.
Vitesse du mouvement réel
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes. Elle vous permet de déplacer les objets dans les diagrammes à des vitesses variables.
Cliquez et maintenez le curseur enfoncé.
Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement. Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Cette barre de défilement contrôle les mouvements des trois objets dans le diagramme ainsi que ceux des nœuds. Vous pouvez les déplacer dans une seule direction – la direction à laquelle les objets se déplacent réellement.
Mouvement réel
Cette barre de défilement fait la même chose que celle pour la vitesse, mais elle couvre le cours d’un seul mois.
Vitesse du mouvement apparent
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes. Elle vous permet de déplacer les objets dans les diagrammes à des vitesses variables.
Cliquez et maintenez le curseur enfoncé.
Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement. Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Cette barre de défilement permet de garder la Terre immobile, et fait tourner le ciel au complet tout comme on peut l’observer dans nos vies quotidiennes. Mais si vous le tournez suffisamment, vous verrez que la Lune et le Soleil se déplacent aussi dans leurs orbites – en se basant sur leurs mouvements réels! Vous pouvez seulement les faire bouger dans une direction – la direction à laquelle les choses semblent réellement bouger.
Mouvement apparent
Cette barre de défilement fait la même chose que celle pour la vitesse, mais elle couvre seulement le cours d’un jour.
Quelque chose de plus
On a vu comment la Lune, le Soleil et les étoiles semblent se déplacer pendant le cours d’une soirée, à cause de la rotation de la Terre. Quand les astronomes utilisent un télescope pour observer une étoile ou un autre objet dans le ciel, la Terre qui tourne amènerait normalement cette étoile à être transportée rapidement en-dehors de notre champ de vision. Les astronomes compensent pour cela en utilisant des moteurs d’entraînement pour faire tourner lentement leurs télescopes dans la direction opposée de celle de la rotation de la Terre. Ça garde les choses bien centrées et leur évite de devoir continuellement ajuster manuellement l’orientation du télescope.
La Terre toujours à une seule et même vitesse constante, alors toutes les étoiles se déplacent dans le ciel à la même vitesse angulaire. Les montures de télescope sont conçues de manière à ce que le moteur d’entraînement puisse tourner à la même vitesse, et cette vitesse de mouvement compensatoire fonctionnera pour toute étoile ou tout objet loin dans le ciel qu’un astronome pourrait vouloir étudier.
Parce que la Lune se déplace si loin dans son orbite à chaque jour, la combinaison de la rotation de la Terre et de l’orbite de la Lune rend les mouvements apparents de la Lune juste un peu plus lents que ceux des étoiles. Si notre astronome utilise pour le télescope un moteur d’entraînement standard qui fonctionne parfaitement pour les étoiles, alors pendant environ 15 minutes d’observation, le moteur ne suffira pas pour empêcher la Lune de dériver à travers le champ de vision. Alors, les moteurs d’entraînement des télescopes ont besoin d’avoir un réglage « lunaire » séparé et plus lent qui doit être utilisé pour observer la Lune!
Ce que vous pouvez apprendre :
- Vous pouvez voir pourquoi les objets dans le ciel semblent se lever à l’est et se coucher à l’ouest.
- Vous pouvez apprendre que la Lune et le Soleil se déplacent en fait réellement d’ouest en est.
- Vous pouvez apprendre que ceci ne change pas avec votre emplacement sur la Terre ou le moment de l’année.
- Vous pouvez voir comment la Lune se déplace contre l’arrière-plan d’étoiles pendant le cours de plusieurs jours.
Les bases de la précession
Voici les bases de la précession de l’orbite de la Terre!
Consultez les instructions du diagramme 11Refermer les instructions
Diagramme 11 :
Les bases de la précession
Ce que vous regardez :
Nous retournons aux étoiles et aux constellations de base pour l’instant, mais nous avons ajouté deux cercles près des deux pôles célestes. Ce sont les « cercles de précession ». Le cercle gris pour l’horizon est présent lui aussi.
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Montrer l’observateur
Si vous cochez cette case, vous verrez un observateur, un petit bonhomme vert, se tenir sur le dessus de la Terre.
L’horizon qu’on a tracé avec le disque gris et le cercle bleu représentent l’horizon que cet observateur pourrait voir. Décochez la case pour cacher l’observateur.
Réinitialiser l’horizon
Il n’est pas toujours facile d’obtenir exactement la vue que vous voulez. Utilisez ce bouton pour réinitialiser l’horizon.
Réinitialiser la date
La barre de défilement « précession » couvre vraiment BEAUCOUP d’années! Au cas où vous auriez de la difficulté à retourner à une année près de l’année actuelle,
utilisez ce bouton pour réinitialiser l’année à celle qui est en cours sur votre appareil.
Tourner la terre
Vous pouvez tourner la Terre pour placer l'observateur exactement à l'endroit où vous vous trouvez maintenant.
Ceci vous permettra de voir les objets dans le ciel exactement comme ils apparaissent là où vous êtes présentement.
Le nombre qui apparaît à la droite de cette barre de défilement représente la longitude de l'endroit où se trouve l'observateur.
Précession
Il s’agit de la barre de défilement la plus importante de ce diagramme! Lorsque ce diagramme se chargera,
vous verrez que ce curseur indiquera une année très près de celle en cours. Pour des raisons en-dehors du but premier de cette discussion,
la Terre oscille lentement sur son orbite pendant des milliers d’années. On appelle cette oscillation « précession »,
et ça amène toute la grille AD/Dec dans le ciel à se déplacer. Encore plus important, ça amène le PNC et le PSC à se déplacer en un cercle,
et les pôles effectuent une révolution complète autour de ces cercles à chaque 25.772 années (à peu près!). En déplaçant le curseur à gauche et à droite,
vous pouvez voir où les pôles ont déjà été, ainsi que où ils seront dans le futur. Il est intéressant de voir où le PNC était situé à
l’époque où les pyramides ont été construites;
vous pouvez lire à propos de comment elles sont alignées avec les points cardinaux
comme ils étaient il y a des milliers d’années - points qui étaient très différents de ceux d’aujourd’hui!
(Il y a aussi des écarts similaires qui ont été découverts à des sites archéologiques à Stonehenge et en Mésoamérique.)
Nous allons aussi aborder quelques sujets additionnels dans les prochains diagrammes.
Comme dans les diagrammes précédents, si vous cliquez sur la barre de défilement de la précession, vous pourrez utiliser les flèches de votre clavier pour vous déplacer lentement à travers les années. Vous ne verrez pas beaucoup de différences d’une année à l’autre, mais vous allez certainement voir les choses changer sur des centaines ou des milliers d’années!
Nous avons centré le curseur de la barre de défilement « précession » à l’époque actuelle (c’est-à-dire, aujourd’hui!), et nous l’avons configuré pour que vous ne puissiez pas aller à des centaines de milliers d’années dans le passé ou le futur. C’est parce que les scientifiques ne sont pas certains que nos observations actuelles puissent correspondre de manière fiable à des dates qui sont si éloignées du présent. On tente tout simplement de vous montrer le concept de la précession – et non pas de prédire ce à quoi le ciel pourrait avoir ressemblé à l’époque des dinosaures!
Latitude
Comme avant, cette barre de défilement permet de déplacer votre vue à une latitude différente sur la Terre.
Ceci vous permet de voir comment les changements dans la précession ont eu des effets sur les étoiles circumpolaires du Nord et du Sud.
Vitesse du temps
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes. Elle vous permet de déplacer les objets dans les
diagrammes à des vitesses variables.
Cliquez et maintenez le curseur enfoncé.
Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement. Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Cette barre de défilement contrôle les mouvements des étoiles qui se déplacent à travers le ciel dans leur trajectoire (apparente) quotidienne autour de la Terre.
Temps sidéral
Cette barre de défilement fait exactement la même chose qu’avant – elle déplace les étoiles à travers le ciel pendant le cours d’une journée.
Mais cette fois, si vous avez changé la date en utilisant la barre de défilement de la précession, les étoiles se retrouveront dans leurs NOUVELLES coordonnées
de la grille AD/Dec! Tout ce qu’on a dit dans les diagrammes précédents à propos de l’AD et de la Dec s’applique ici, sauf que vous devez vous rappeler que les
étoiles auront de nouvelles coordonnées alors qu’on s’éloigne dans le temps.
Des étoiles différentes pourraient alors devenir circumpolaires!
Ce que vous pouvez apprendre :
- Vous pouvez visualiser la « précession » de l’axe de rotation de la Terre.
- Vous pouvez voir comment l’AD et la Dec des étoiles change sur de très nombreuses années.
- Vous pouvez apprendre pourquoi les grands monuments astronomiques des civilisations anciennes sont précisément alignées à des points cardinaux qui n’existent plus.
La trajectoire de la précession des pôles de la Terre à travers le ciel
On a ajouté les constellations près du pôle nord céleste (PNC) et du pôle sud céleste (PSC)
pour que vous puissiez voir comment les pôles de la Terre se déplaceront à travers les étoiles.
Consultez les instructions du diagramme 12Refermer les instructions
Diagramme 12 :
La trajectoire de la précession des pôles de la Terre à travers le ciel
Ce que vous regardez :
C’est la même chose que le diagramme 11, mais on a ajouté des constellations près des pôles célestes. Ceci vous montrera les trajectoires du cercle de précession à travers l’actuel champs d’étoiles.
Vous pouvez cliquer sur n’importe quelle étoile dans ces constellations pour voir le nom de cette constellation.
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Montrer l’observateur
Si vous cochez cette case, vous verrez un observateur, un petit bonhomme vert, se tenir sur le dessus de la Terre.
L’horizon qu’on a tracé avec le disque gris et le cercle bleu représentent l’horizon que cet observateur pourrait voir. Décochez la case pour cacher l’observateur.
Réinitialiser l’horizon
Il n’est pas toujours facile d’obtenir exactement la vue que vous voulez. Utilisez ce bouton pour réinitialiser l’horizon.
Réinitialiser la date
La barre de défilement « précession » couvre vraiment BEAUCOUP d’années! Au cas où vous auriez de la difficulté à retourner à une année près de l’année actuelle,
utilisez ce bouton pour réinitialiser l’année à celle qui est en cours sur votre appareil.
Tourner la terre
Vous pouvez tourner la Terre pour placer l'observateur exactement à l'endroit où vous vous trouvez maintenant.
Ceci vous permettra de voir les objets dans le ciel exactement comme ils apparaissent là où vous êtes présentement.
Le nombre qui apparaît à la droite de cette barre de défilement représente la longitude de l'endroit où se trouve l'observateur.
Précession
C’est la même chose que dans le diagramme 11! Au cas où vous ne l’auriez pas encore vu, en voici les explications :
Nous allons aussi aborder quelques sujets additionnels dans les prochains diagrammes.
Comme dans les diagrammes précédents, si vous cliquez sur la barre de défilement de la précession, vous pourrez utiliser les flèches de votre clavier pour vous déplacer lentement à travers les années. Vous ne verrez pas beaucoup de différences d’une année à l’autre, mais vous allez certainement voir les choses changer sur des centaines ou des milliers d’années!
Nous avons centré le curseur de la barre de défilement « précession » à l’époque actuelle (c’est-à-dire, aujourd’hui!), et nous l’avons configuré pour que vous ne puissiez pas aller à des centaines de milliers d’années dans le passé ou le futur. C’est parce que les scientifiques ne sont pas certains que nos observations actuelles puissent correspondre de manière fiable à des dates qui sont si éloignées du présent. On tente tout simplement de vous montrer le concept de la précession – et non pas de prédire ce à quoi le ciel pourrait avoir ressemblé à l’époque des dinosaures!
Latitude
Comme avant, cette barre de défilement permet de déplacer votre vue à une latitude différente sur la Terre.
Ceci vous permet de voir comment les changements dans la précession ont eu des effets sur les étoiles circumpolaires du Nord et du Sud.
Vitesse du temps
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes. Elle vous permet de déplacer les objets dans les
diagrammes à des vitesses variables.
Cliquez et maintenez le curseur enfoncé.
Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement.
Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Cette barre de défilement contrôle les mouvements des étoiles qui se déplacent à travers le ciel dans leur trajectoire (apparente) quotidienne autour de la Terre.
Temps sidéral
Cette barre de défilement fait exactement la même chose qu’avant – elle déplace les étoiles à travers le ciel pendant le cours d’une journée.
Mais cette fois, si vous avez changé la date en utilisant la barre de défilement de la précession, les étoiles se retrouveront dans leurs NOUVELLES coordonnées
de la grille AD/Dec! Tout ce qu’on a dit dans les diagrammes précédents à propos de l’AD et de la Dec s’applique ici, sauf que vous devez vous rappeler que les
étoiles auront de nouvelles coordonnées alors qu’on s’éloigne dans le temps.
Des étoiles différentes pourraient alors devenir circumpolaires!
Ce que vous pouvez apprendre :
- Vous pouvez visualiser la « précession » de l’axe de rotation de la Terre.
- Vous pouvez voir comment les étoiles changent d’AD et de Dec sur de très nombreuses années.
- Vous pouvez apprendre pourquoi les monuments astronomiques des grandes civilisations anciennes sont précisément alignés avec des points cardinaux qui n’existent plus.
- Vous pouvez voir pourquoi Polaris est seulement temporairement l'étoile polaire de l'hémisphère nord, et pourquoi l'hémisphère sud finira par avoir à son tour sa propre étoile polaire.
Les effets de la précession sur les saisons et le premier point du Bélier
On vous ramène le zodiaque et l’écliptique pour que vous puissiez
voir comment la précession pourrait changer le cours des choses sur le long terme!
Consultez les instructions du diagramme 13Refermer les instructions
Diagramme 13 :
Les effets de la précession sur les saisons et le premier point du Bélier
Ce que vous regardez :
Maintenant, le Soleil et l’écliptique sont de retour, tout comme les constellations du zodiaque. Toutes les fonctions de la précession sont aussi en place, pour que nous puissions voir ce qui pourrait arriver pendant une longue période de temps.
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Réinitialiser l’horizon
Il n’est pas toujours facile d’obtenir exactement la vue que vous voulez. Utilisez ce bouton pour réinitialiser l’horizon.
Réinitialiser la date
La barre de défilement « précession » couvre vraiment BEAUCOUP d’années! Au cas où vous auriez de la difficulté à retourner à une année près de l’année actuelle,
utilisez ce bouton pour réinitialiser l’année à celle qui est en cours sur votre appareil.
Précession
C’est la même chose que dans les diagrammes 11 et 12. Voici ce qu’on a déjà dit avant à propos de la précession :
Il s’agit de la barre de défilement la plus importante de ce diagramme! Lorsque ce diagramme se chargera,
vous verrez que ce curseur indiquera une année très près de celle en cours. Pour des raisons en-dehors du but premier de cette discussion,
la Terre oscille lentement sur son orbite pendant des milliers d’années. On appelle cette oscillation « précession »,
et ça amène toute la grille AD/Dec dans le ciel à se déplacer. Encore plus important, ça amène le PNC et le PSC à se déplacer en un cercle,
et les pôles effectuent une révolution complète autour de ces cercles à chaque 25 772 années (à peu près!). En déplaçant le curseur à gauche et à droite,
vous pouvez voir où les pôles ont déjà été, ainsi que où ils seront dans le futur. Il est intéressant de voir où le PNC était situé à
l’époque où les pyramides ont été construites;
vous pouvez lire à propos de comment elles sont alignées avec les points cardinaux
comme ils étaient il y a des milliers d’années - points qui étaient très différents de ceux d’aujourd’hui!
(Il y a aussi des écarts similaires qui ont été découverts à des sites archéologiques à Stonehenge et en Mésoamérique.)
Nous allons aussi aborder quelques sujets additionnels dans les prochains diagrammes.
Comme dans les diagrammes précédents, si vous cliquez sur la barre de défilement de la précession, vous pourrez utiliser les flèches de votre clavier pour vous déplacer lentement à travers les années. Vous ne verrez pas beaucoup de différences d’une année à l’autre, mais vous allez certainement voir les choses changer sur des centaines ou des milliers d’années!
Nous avons centré le curseur de la barre de défilement « précession » à l’époque actuelle (c’est-à-dire, aujourd’hui!), et nous l’avons configuré pour que vous ne puissiez pas aller à des centaines de milliers d’années dans le passé ou le futur. C’est parce que les scientifiques ne sont pas certains que nos observations actuelles puissent correspondre de manière fiable à des dates qui sont si éloignées du présent. On tente tout simplement de vous montrer le concept de la précession – et non pas de prédire ce à quoi le ciel pourrait avoir ressemblé à l’époque des dinosaures!
Jour de l’année
Comme dans les diagrammes précédents, ceci vous permet de déplacer le Soleil à travers le zodiaque – en définissant un jour de l’année.
Mais maintenant, nous avons intégré la fonction supplémentaire de la précession.
Ceci vous permet de voir comment le premier point du Bélier, l’écliptique et les saisons elles-mêmes se déplacent à travers les mois sur de longues périodes de temps…
...ou plutôt, comme ceux-ci se déplaceRAIENT, s’il n’y avait pas notre système de calendrier actuel.
C’est exact! Le système actuel ajoute des journées bissextiles à certaines années, et est soigneusement conçu pour ÉVITER que les saisons se décalent au fil des siècles. Dans notre diagramme, nous tenons compte uniquement d’une année de 365 jours. Comme on le sait, à chaque quatre ans, nous ajoutons une journée bissextile dans une année, soit le 29 février. Cela empêche les saisons d’avancer lentement dans le calendrier, et assure que le décalage que nous voyons dans ce diagramme n’aura pas réellement lieu.
Mais pourquoi l’avons nous fait ainsi alors? Et pourquoi n’avons nous pas un diagramme qui montre ce qui se passe réellement? Et bien, nous l’avons fait ainsi parce qu’il est important de comprendre pourquoi ces journées bissextiles sont essentielles, et pour montrer ce qui est arrivé dans le passé quand nous ne les avions pas. Nous ne pouvons pas montrer un diagramme qui explique comment le calendrier empêche ce décalage, parce qu’il n’y aurait pas vraiment grand-chose qui se passerait! Même sur des milliers d’années, l’écliptique et les saisons se déplaceraient à peine – et ça ferait un diagramme très ennuyant.
Parlons un peu de ce calendrier, et du système des journées bissextiles. Premièrement, il y a plus de 365 jours dans une année. Cela prend 365 jours et quart pour que la Terre fasse le tour complet du Soleil. Alors, en ajoutant une journée bissextile à chaque quatre ans, cela compense pour le quart de journée qui serait perdu autrement.
Bien sûr, l’orbite de la Terre n’est pas exactement de 365,25 jours. Cela serait bien trop facile! Ce nombre est juste un tout petit peu plus grand que le nombre réel. Nous ne pouvons pas ajouter continuellement des journées bissextiles à chaque quatre ans. Sinon, nous aurions exactement le même décalage qu'on tente d'éviter dans le calendrier. En faisant cela, nous finirions avec trois journées d’avance à chaque 400 ans. Alors, on s’est occupé de cela dans le calendrier en faisant en sorte que chaque dernière année d’un siècle (1700, 1800, 1900) ne soit pas une année bissextille, à moins qu’elle ne soit divisible par 400. Cela veut dire que les années comme 1700, 1800 et 1900 n’étaient pas des années bissextiles – mais 1600 et 2000 l’étaient. 2100, 2200 et 2300 ne seront pas des années bissextiles, mais 2400 le sera – et ainsi de suite. Ce petit ajustement pour la règle de « à chaque quatre ans » est tout ce dont nous avons de besoin pour rendre le calendrier plus précis, du moins jusqu’à ce que nous atteignions approximativement l’année 4500 (à ce moment-là, ce sera le problème de quelqu’un d’autre!) Rendu là, d’autres facteurs entreront en jeu et rendront certains ajustements nécessaires.
En passant, ce système complexe-mais-précis de journées bissextiles a été mis en place en octobre 1582. Le pape Grégoire XIII en était un partisan et a défendu cette idée, ainsi notre calendrier est donc connu à ce jour comme étant le calendrier « grégorien ».
Tourner la Terre
Ceci fait ce que ça a toujours fait – ça fait tourner la Terre pour que vous puissiez placer la partie que vous voulez sous la lumière du jour.
Ce que vous pouvez apprendre :
- Vous pouvez visualiser la « précession » de l’axe de rotation des pôles de la Terre alors qu’ils se déplacent à travers les constellations circumpolaires.
- Vous pouvez voir comment l’écliptique – et donc, les saisons – évoluerait sur de nombreuses années.
- Vous pouvez apprendre pourquoi notre calendrier grégorien est si pratique, et si nécessaire.
Parallaxe
Apprenez les bases d’une méthode pour mesurer la distance entre les étoiles les plus proches!
Consultez les instructions du diagramme 14Refermer les instructions
Diagramme 14 :
Parallaxe
Ce que vous regardez :
Il n’y a pas de sphère dans ce diagramme. Vous regardez deux plaques plates. Une est une plaque horizontale à l’avant-plan, contenant le Soleil et la Terre. L’autre est une plaque verticale au loin en arrière-plan, contenant des étoiles plus éloignées.
Le but de ce diagramme est de vous montrer une méthode que les astronomes utilisent pour mesurer la distance avec des étoiles qui sont relativement proches de nous. C’est un peu la même situation que lorsque vous levez un doigt en l’air à une longueur de bras de distance et que vous regardez des objets éloignés en fermant un œil, puis en fermant l’autre œil. Votre doigt semblent sauter ou se déplacer par rapport à l’objet que vous regardez. Plus vous approchez votre doigt de votre visage, plus il semble « sauter » loin.
Dans cet exemple, l’étoile rouge la plus proche est comme votre doigt. Vos yeux gauche et droit représentent la vue qu’on a de cette étoile quand la Terre est sur des côtés opposés de son orbite autour du Soleil. Pour faire cette expérience, on doit prendre une mesure de la position de l’étoile rouge avec en arrière-plan des étoiles plus éloignées. Ensuite, six mois plus tard, on reprend la même mesure pour voir comment l’étoile-cible semble s’être déplacée – comment elle a « sauté » à travers le décor. Un peu de géométrie fait le reste, et on obtient une bonne idée de la distance approximative de l’étoile rouge!
(De pouvoir obtenir des résultats aussi précis avec des mathématiques si simples est assez incroyable. La plupart des calculs en astronomie impliquent du calcul différentiel et des principes physiques très compliqués. Il est donc agréable de voir des résultats aussi importants que la distance des étoiles être réduits à quelque chose que nous pouvons tous comprendre à l’aide de nos mathématiques du secondaire!)
De retour à la réalité : pour pouvoir faire ce calcul de manière précise, nous devons pouvoir mesurer la position relative des étoiles de manière très précise : le saut ou le déplacement qu’on observe dans la position de l’étoile représente une distance qui est loin d’être aussi grande qu’elle ne semble l’être dans ce diagramme! Aussi, nous devons utiliser comme arrière-plan des étoiles qu’on connaît comme étant très éloignées – et elles doivent être en arrière-plan du champ de vision de notre étoile-cible. L’étoile qu’on mesure doit être aussi être relativement très proche de nous – la méthode ne fonctionnera pas pour des étoiles éloignées, puisque la distance de déplacement qu’on observerait ne serait pas suffisante pour effectuer une mesure adéquate. Cette méthode est toutefois une méthode qui a déjà été utilisée, et c’est tout ce que nous avions jusqu’à ce que plusieurs des grandes découvertes cosmologiques du début du 20e siècle soient faites.
Finalement, nous désirons partager avec vous un fait peu connu de la plupart des gens. Pendant une éclipse totale, les gens se trouvant dans la bande étroite de la totalité de l’éclipse voient la Lune passer directement en avant du Soleil. Les gens sur la Terre qui se trouvent à seulement quelques kilomètres en-dehors de cette bande étroite verront la Lune passer « au-dessus » ou « en-dessous » du Soleil dans le ciel, et ils ne verront pas la totalité de l’éclipse. C’est à cause de la parallaxe! C’est vrai, la position de la Lune dans le ciel que vous pouvez voir où vous vous trouvez varie de beaucoup, selon votre emplacement sur la Terre. Alors, même si la pleine Lune pourrait être en train de se lever pour vous tôt le matin, au même moment, pour quelqu’un situé de l’autre côté de la Terre, la Lune serait en train de se coucher et ce serait le soir. Vous pouvez être certain que l’emplacement de la Lune dans le ciel par rapport aux étoiles en arrière-plan est très différent pour vous deux.
Contrôles :
Vous pouvez toujours utiliser le bouton de gauche de la souris pour faire bouger le diagramme en deux dimensions si vous désirez le voir de haut en bas ou de côté.
Distance de l'étoile proche
Vous pouvez déplacer l’étoile rouge pour qu’elle soit plus proche ou plus éloignée de la Terre, et voir comment ses mouvements changent sur une période de six mois. Si vous la déplacez trop près,
elle va sortir de l’écran (de toute manière, il n’y a pas d’étoiles qui sont si proches de nous dans le vrai ciel!). Si vous la déplacez trop loin, elle sera à la même distance que les
étoiles en arrière-plan. La méthode de calcul va alors échouer, car l’étoile ne « sautera » pas assez entre deux observations.
On doit aussi prendre en note qu’on a utilisé des étoiles de la constellation de l’Orion pour nos étoiles « éloignées » en arrière-plan. Les étoiles de l’Orion sont généralement relativement assez loin – mais pour faire cette expérience dans la vraie vie, il faudrait choisir des étoiles moins brillantes beaucoup plus loin de nous que les célèbres étoiles de l’Orion qui sont situées à peine à quelques centaines d’années-lumière de nous.
Jour de l’année
Ici, vous pouvez déplacer la Terre de gauche à droite dans son orbite autour du Soleil et ainsi voir les triangles formés par ce déplacement. Une fois que la Terre est complètement à gauche
(avec le curseur de la barre de défilement complètement à droite), alors un ensemble de deux triangles semblables est formé.
À ce stade-ci, vous pourriez utiliser de la simple géométrie pour estimer la distance avec votre étoile-cible. Gardez à l’esprit que ce sont ici des angles extrêmement petits qui sont en jeu -
des angles beaucoup plus petits qu’une seconde d’arc, qui est 1800 fois plus petite qu’une pleine Lune! (Plus à propos de ça dans le diagramme 16, mais nous allons vous expliquer ici qu’une seconde
d’arc est à peu près de la même taille que si vous regardiez un petit pois situé à une distance d’environ 700 verges [650 mètres]!)
Alors vous devez être capables d’effectuer des mesures avec une précision qui n’est pas facile à atteindre à partir de votre cour arrière.
Il y a une autre chose que nous souhaitons mentionner. Si vous regardez de très près, vous verrez que dans notre diagramme, alors que la Terre se déplace autour du Soleil, la projection de l’étoile rouge contre les étoiles lointaines semble dépasser légèrement à gauche et droite les limites de la région du ciel où elle finit par s’établir. On s’attend à cet effet, parce que la Terre rejoint des points dans son orbite où l'étoile semble se déplacer en-dehors de l'endroit où elle apparaît lorsque la Terre atteint les extrémités de son orbite. Dans la vraie vie, cette différence est minuscule. Si nous devions essayer d’utiliser ces deux emplacements situés aux extrémités pour faire l’expérience, nous aurions besoin de savoir à l’avance à quelle distance se trouve l’étoile rouge – ce qu’on ne sait pas. Il est plus facile de former deux triangles autant que possible parfaitement isocèles. Pour ça, on doit utiliser deux positions de la Terre situées à des extrémités parfaitement opposées de son orbite.
Dans notre diagramme, nous avons aussi utilisé une durée de 183 jours comme étant la durée approximative d’une moitié d’orbite de la Terre. En réalité, nous devrions utiliser des mesures prises exactement aux moments mêmes où la Terre atteint les extrémités de son orbite pour l’année de notre observation, de même que l’emplacement de notre étoile-cible dans le ciel. Nous devrions aussi tenir compte de la distance changeante entre la Terre et le Soleil pendant le cours d’une année.
Alors, comme pour tout le reste en astronomie, la réalité est un peu plus compliquée que le portrait simplifié qu’on peut en faire. Ce diagramme est conçu uniquement pour vous donner une idée de base de ce que cette expérience implique.
Quelque chose de plus
En 2020, les astronomes de la NASA ont utilisé la sonde New Horizons pour obtenir de nouvelles informations à propos de la parallaxe de deux des plus proches étoiles.
Après avoir visité Pluton et l’objet 486958 Arrokoth dans la ceinture de Kuiper, New Horizons poursuit sa course dans l’espace lointain. En avril 2020, la sonde était à 6,9 milliards de kilomètres
de la Terre.
Ceci a donné aux astronomes une opportunité unique d’employer la méthode de la parallaxe en utilisant un triangle avec une base beaucoup plus large que ce que l’orbite de la Terre aurait pu fournir.
Des photographies des étoiles Proxima Centauri et Wolf 359 ont été prises par New Horizons et comparées avec celles prises ici sur la Terre. Comme on pouvait s’y attendre, ces deux étoiles proches ont démontré un grand décalage parallactique par rapport à l’arrière-plan formé d’étoiles lointaines. Les mesures ont été utilisées pour confirmer ce qu’on savait déjà à propos de leurs distances. On a confirmé une distance de 4,2 années-lumière de la Terre pour Proxima Centauri. Wolf 359 est un peu plus éloignée à 7,9 années-lumière!
Ce que vous pouvez apprendre :
- Vous pouvez voir les bases de comment les astronomes mettraient en place une expérience sur la parallaxe pour mesurer la distance avec une étoile proche.
- Vous pouvez voir comment cette expérience utilise des mesures précises, mais des mathématiques très simples, pour faire son travail!
Le jour sidéral et le jour solaire
Voici un modèle pour vous montrer pourquoi il y a une différence entre le jour sidéral et le jour solaire.
Consultez les instructions du diagramme 15Refermer les instructions
Diagramme 15 :
Jour sidéral vs jour solaire
Ce que vous regardez :
Vous voyez l’orbite de la Terre autour du Soleil, comme si vous étiez au-dessus d’eux. Alors que la planète effectue une orbite complète, vous pouvez voir la différence entre ce qu’on appelle le jour « sidéral » vs le jour « solaire ». Le Soleil est le cercle jaune dans le milieu. L’avertissement qu’on peut lire à propos de plusieurs modèles astronomiques s’applique ici : « le diagramme n’est PAS à l’échelle! »
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme.
Basculer sidéral/solaire
Ce bouton vous permet de basculer entre le jour sidéral et solaire selon où vous vous trouvez dans l’orbite de la Terre. Par exemple, si vous déplacez le curseur pour observer la position
de la Terre après 100 jours sidéraux, alors ce bouton vous amènera à la position après 100 jours solaires.
Vous pouvez basculer entre les deux vues pour que la différence entre les deux types de jours soit encore plus facile à voir.
Le seul endroit où le nombre de jours sidéraux et solaires ne seront PAS égaux est à la toute fin de l’ « année » - où vous pouvez voir que 366 jours sidéraux est égal à 365 jours solaires.
Barres de défilement du jour sidéral et du jour solaire
Ces barres de défilement sont tellement interconnectées que nous allons décrire leurs actions pour les deux ensemble. La plupart des diagrammes qui montrent ce concept sont vraiment simplifiés.
Nous voulions vous montrer comment la différence entre les deux types de jours affecte considérablement les choses au cours d’une année.
Un peu de contexte
Définissons d’abord ce que nous entendons par chaque type de journée :
Jour solaire
Nous avons l’habitude d’utiliser des jours « solaires » dans nos vies quotidiennes. En général, une journée solaire équivaut à la mesure entre le moment où le Soleil est haut dans le ciel (comme à midi) jusqu’au moment où il est de nouveau haut dans le ciel le jour suivant (aussi à midi). Ceci semble être une manière très logique de définir un « jour », mais il y a des complications. Pour commencer, il y a le fait que le moment exact qui correspond à « midi » change selon où on se trouve sur la Terre. Des gens se trouvant à des longitudes légèrement différentes vont vivre avec des heures solaires légèrement différentes. Si vous vous trouvez dans une grande ville comme St-Paul au Minnesota, Brooklyn à New York, Bismarck au Dakota du Nord, Surrey BC, Montréal, Toronto, ou Lloydminster SK, alors vous verrez le Soleil atteindre son point le plus haut quelques minutes plus tôt que les gens qui se trouvent directement à l’ouest de vous – donc à Minneapolis, Staten Island, Mandan, Vancouver, Laval, Mississauga ou Lloydminster AB. Le maintien du temps basé sur un tel système serait assez peu pratique, sachant que vous devriez alors tenir compte de l’heure qu’il est dans tous les endroits autour de vous où vos amis et les membres de votre famille pourraient vivre. C’est exactement le problème qu’ont eu les compagnies de chemin de fer, et cela a conduit presque directement à la création de « fuseaux horaires » pour essayer d’uniformiser les choses.
Mais il y a une autre complication dont nous allons parler dans un autre diagramme : l’équation du temps. Le Soleil ne se déplace pas à travers le ciel exactement à la même vitesse pendant tout le cours d’une année. Sa vitesse ne change pas tant que ça, c’est sûr, mais il y a une différence suffisamment grande dans la durée d’un jour solaire réel pour que si vous essayez de garder le temps précis à la minute près, il est tout simplement impossible de ne pas devoir ajuster éventuellement le jour de l’année.
Ce que nous allons faire dans cette discussion (et aussi dans celle à propos de l’équation du temps) est de parler d’une journée solaire « moyenne ». Nous allons imaginer qu’il y a un faux Soleil en haut dans le ciel qui se déplace toujours exactement à la même vitesse. Parfois, ce soleil « moyen » sera en retard par rapport au vrai Soleil, et parfois, il sera en avance. Si on prend en note l’heure où ce soleil « moyen » est à son point le plus haut pour une journée, alors cela va prendre exactement 24 heures avant qu’il ne soit à son point le plus haut le jour suivant. C’est la seule façon de garder les calculs à un niveau raisonnable à ce stade-ci, et ce n’est pas une mauvaise approximation pour l’instant. Si l’absence d’une parfaite précision vous dérange, imaginez que nous parlons du vrai Soleil, et vous ne serez pas loin de la réalité. Le concept s’applique toujours, mais les nombres seront légèrement différents.
(À partir de maintenant, quand on dit « jour solaire », on veut dire « jour solaire moyen ». C’est bon? OK!)
Jour sidéral
Maintenant, que voulez-nous dire par jour « sidéral »? Et bien, on vient juste de parler de la période de temps entre le moment où le Soleil est le plus haut du ciel, et le prochain moment où il sera à son point le plus haut dans le ciel. Mais qu’en est-il des étoiles? Nous avons vu comment les étoiles culminent à différents moments de la journée tout au long de l’année. C’est de là que vient ce décalage. Nous avons l’habitude de mesurer le temps en utilisant le Soleil dans notre vie quotidienne, mais les astronomes voulaient avoir une référence de temps basée sur les étoiles. C’est ici que tout le concept de l’AD est entré en jeu. Ils se sont rendus compte que la Terre tournait assez pour faire passer une étoile donnée d'un point culminant à l'autre en un peu moins de temps que le Soleil a besoin pour passer de son point culminant au prochain point culminant.
C’est parce que pendant cette journée, la Terre a bougé un peu dans son orbite – alors, ça a pris juste un peu plus de temps pour que la Terre tourne sur elle-même jusqu’au moment où le Soleil se retrouve de nouveau à son point le plus haut dans le ciel! Ce n’est pas tant que le « jour de l’étoile » était plus court, c’est plutôt que le « jour du Soleil » était plus long car on n’avait pas pris en compte l’orbite de la Terre. Mais il était trop tard, tout avait déjà été finalisé en se basant sur le Soleil. Les astronomes ont alors dû adapter leur système. (C’est BEAUCOUP plus facile de comprendre ceci en regardant le diagramme plutôt que d’essayer de comprendre les explications écrites!)
Une fois que la Terre a tourné assez sur elle-même pour compléter une journée sidérale entière, combien de temps de plus cela prend-il pour que le Soleil se rende à son point culminant de nouveau? C’est là qu’il est important de prendre en compte la durée complète d’une année, et d’inclure le quart de jour de plus dans nos calculs. Au bout du compte, un jour solaire a 3m 55,91s de plus qu’un jour sidéral, soit un peu moins de 4 minutes.
Quatre minutes, ça ne semble pas beaucoup, mais quand on les additionne, cela peut faire toute une différence! Au bout d’un mois (30 jours x 4 minutes par jour = 120 minutes…), cela représente environ 2 heures! (Rappelez-vous, 2 heures d’AD représentent 30° de mouvement d’étoile, et 360° divisé par 30° par mois nous donne la valeur d’une année complète de 12 mois.) Après une année complète, tout cela s’additionne (365 jours x 4 minutes par jour = environ 24 heures…) et donne une journée complète! C’est vrai, même s’il y a 365 jours « normaux » (et des poussières) dans une année, il y a 366 (!) (et des poussières) jours sidéraux dans une année..
Combien de jours avons-nous dit qu’il y avait dans une année? Si vous avez répondu 365, alors vous devez vous rappeler que la Terre prend 1/4 de jour de plus pour faire complètement le tour du Soleil. C’est un point très important pour notre discussion, même si nous n’allons pas inclure ce jour de plus dans notre diagramme. Nous tentons de comparer ce qui se passe au moment où nous tombons sur chaque jour sidéral ou solaire. Nous ne sommes pas très préoccupés par ce qui se passe pendant cette dernière fraction d’un jour…
...sauf pour le fait que nous n’en avons pas tenu compte, alors notre mesure de 3m 55,91s sera suffisamment décalée pour que nous ayons quelques minutes de décalage d’ici la fin de l’année – ce qui n’est pas bon. Alors nous allons conserver la précision de cette mesure pendant le cours d’une année, mais nous allons cesser cette expérience un peu avant la fin d’une année complète. Nous offrons nos excuses sincères aux astronomes qui s’époumonent en ce moment devant leurs écrans, horrifiés par ces mesures approximatives – ce sera toutefois suffisant pour ce que nous avons besoin de faire! Encore une fois, nous essayons d’éduquer, pas de créer un éphéméride!
Comment utiliser les barres de défilement
Le diagramme débute sur une journée donnée de l’année, où le Soleil est haut dans le ciel et où une certaine étoile ou certaines étoiles apparaissent juste en arrière dans le ciel. Bien sûr, vous ne pouvez pas voir ces étoiles, parce que non seulement c’est le milieu de la journée, mais en plus elles sont cachées en arrière du Soleil! Le jour exact de l’année ou notre emplacement précis sur la Terre n’est pas important ici. Ce qui compte, c’est de choisir un moment où le Soleil est à son point le plus haut dans le ciel et où certaines étoiles sont exactement dans la même direction dans le ciel que le Soleil. C’est comme ça que débute notre expérience.
Appelez le jour où débute notre expérience le « jour 0 ». À partir d’ici, vous pouvez utiliser n’importe quelle barre de défilement pour choisir le moment de l’année que vous souhaitez. Lorsque vous déplacez un curseur, l’autre curseur bougera aussi en même temps. Lorsque vous arrêtez un curseur, vous tomberez soit sur un jour solaire ou un jour sidéral (selon le curseur que vous avez déplacé). L’autre barre de défilement vous montrera alors l’équivalent dans l'autre type de jour. Par exemple, si vous déplacez le curseur pour le jour sidéral à 100 jours sidéraux, alors vous verrez que la barre de défilement pour le jour solaire indiquera 99,73 jours solaires. La Terre a alors tourné 100 fois par rapport aux étoiles (qui sont bien loin, au-dessus du sommet du diagramme). Par contre, la Terre ne s’est pas encore rendue assez loin dans son orbite pour que le Soleil soit directement au-dessus de nous dans le ciel pour que le 100e jour solaire soit complété. Il reste encore environ un quart de jour à compléter pour ainsi se rendre au 100e jour solaire.
Vous pouvez voir que la différence entre les deux jours est très précise; dans ce cas, la Terre doit encore tourner pendant 6h33m11,0s pour se rendre à ce 100e jour solaire. Alors, après 100 jours, ce petit 3m 55,91s de différence représente maintenant 6 heures et demie! Les étoiles qui ont culminé à minuit il y a 100 jours culminent maintenant vers 17h30. Ça veut dire qu’elles se couchent à peu près vers minuit.
Nous avons ajouté une belle petite fonction qui vous permet de voir cette différence encore plus facilement. Regardez le petit point rouge sur la Terre, et comment il est du côté « supérieur » de la Terre, pointant vers les étoiles en haut au loin? C’est parce que vous avez déplacé le curseur pour le jour sidéral, alors tout est basé sur l’emplacement des étoiles dans le ciel d’un jour à l’autre. Maintenant, si vous cliquez sur le bouton « Basculer sidéral/solaire », vous verrez la Terre tourner sur elle-même pour l’équivalent de six heures de rotation. En cliquant sur ce bouton, le point rouge sera maintenant pointé vers le Soleil maintenant, nous parlons de jours solaires. Vous verrez qu’avec ces six heures de rotation supplémentaires, le diagramme va montrer la situation après 100 jours solaires, ce qui est la même chose que 100,27 jours sidéraux. Nous nous sommes déplacés de six heures dans le futur – un quart de jour. À cause de ça, la différence entre les deux jours a maintenant augmenté d’un peu plus d’une minute – ce qui est à peu près le quart de la différence quotidienne entre les deux types de jours!
Vous pouvez alterner entre 100 jours solaires et 100 jours sidéraux autant que vous voulez et ainsi voir la différence que quatre petites minutes peut faire. Plus on avance dans l’année, plus la différence sera grande entre les jours solaires et sidéraux!
Plusieurs diagrammes vont seulement montrer cette différence pour un jour donné. Ici, vous pouvez déplacer les curseurs des barres de défilement où vous voulez n’importe où dans l’année. Alors que vous déplacez la Terre plus loin dans son orbite, vous verrez que la différence entre x nombre de jours solaires et x nombre de jours sidéraux augmente continuellement. Après une année complète, le total de cette différence sera l’équivalent d’une journée complète.
Ce que vous pouvez apprendre :
- Vous pouvez voir la différence entre un jour sidéral et un jour solaire pour n’importe quel point de l’orbite de la Terre.
- Vous pouvez voir comment cette différence s’additionne tout au long de l’année.
- Vous pouvez apprendre pourquoi ces deux méthodes différentes pour déterminer la durée d’un « jour » ont été créées.
Distances en astronomie - Définitions
Voici quelques illustrations simples à propos des unités de mesure de distance les plus élémentaires utilisées en astronomie.
Consultez les instructions du diagramme 16Refermer les instructions
Diagramme 16 :
Distances en astronomie - Définitions
Ce que vous regardez :
Voici six images simples pour vous montrer les définitions de six unités de mesure de distance différentes utilisées par les astronomes.
Contrôles :
Il y a une seule commande : On vous a donné une barre de défilement pour que vous puissiez vous déplacer entre les différentes définitions. Alors que vous déplacez le curseur vers la droite, les distances affichées deviennent plus grandes.
Nous allons utiliser les termes correspondant à ces unités de mesure de distance dans les prochains diagrammes, alors vous devez vous familiariser avec eux!
Pour votre information, le terme « parsec » n’est pas très utilisé, mais il est très pratique pour les astronomes qui s’occupent de la séparation angulaire entre des étoiles qui sont très proches une de l’autre. Que veut-on dire par « séparation angulaire »? Et bien, vous ne pouvez pas vraiment dire que des objets dans le ciel ont tant de « pouces » ou de « millimètres » entre eux. Ça ne fait pas non plus de sens de parler de combien de kilomètres ou d’années-lumière il y a entre ces objets, vu que cela ne nous indique pas vraiment quelle distance il semble y avoir entre eux dans le ciel.
Donc, les astronomes utiliseront des degrés pour parler de la séparation entre les objets – les mêmes degrés que nous avons appris dans nos cours de maths, pour lesquels il y a 360° dans un cercle complet. Cela veut dire qu’il y a 90° entre l’horizon et le point situé directement au-dessus de nous (appelé le « zénith »). Aussi, la Lune et le Soleil semblent avoir depuis la Terre un diamètre d’environ un demi-degré.
Un degré est divisé en 60 « minutes » d’arc, et chaque minute est divisée en 60 « secondes » d’arc. Comme vous pouvez l’imaginer, une seconde d’arc est très petite. Si deux étoiles sont déparées par 1 seconde d’arc, vous ne pourriez même pas les voir comme étant deux étoiles différentes. En fait, plusieurs personnes ont de la difficulté à voir deux étoiles différentes si elles sont séparées par une minute d’arc complète – ce qui représente 60 secondes d’arc! Mais avec un télescope puissant, il devient possible de « résoudre » des étoiles qui sont très proches une de l’autre. Le parsec est alors utilisé régulièrement lorsque des astronomes doivent parler de ces très petites séparations angulaires.
Ce que vous pouvez apprendre :
- Vous pouvez apprendre à propos des six termes différents que les astronomes utilisent pour décrire les distances dans l’espace.
Distances en astronomie - Exemples
On va vous montrer des exemples de distances entre de véritables objets célestes.
Consultez les instructions du diagramme 17FRefermer les instructions
Diagramme 17 :
DDistances en astronomie - Exemples
Ce que vous regardez :
On vous présente 11 images différentes qui utilisent les termes qu’on vient de vous apprendre. Vous pouvez utiliser la barre de défilement pour passer d’une image à l’autre. Lorsque vous déplacez le curseur vers la droite, les objets (et leurs distances) vont devenir plus grands.
Contrôles :
Curseur principal
Il y a seulement un curseur. Il sert à vous déplacer entre les 11 images différentes fournies. Pour chacune de ces images, on a indiqué une distance en utilisant plusieurs unités de mesure de distance pour que vous puissiez voir les différences possibles.
Ce que vous pouvez apprendre :
- Vous pouvez voir comment différents termes sont utilisés pour les distances, en allant des plus petits aux plus gros objets astronomiques.
Deuxième loi du mouvement de Kepler
Une illustration du mouvement orbital en utilisant des orbites elliptiques réelles.
Consultez les instructions du diagramme 18Refermer les instructions
Diagramme 18 :
Deuxième loi du mouvement de Kepler
Ce que vous regardez :
Voici une vue à « vol d'oiseau » de l'orbite d'un objet autour du Soleil. Il pourrait s’agir d’une planète, d’une comète, d’un vaisseau spatial ou peut-être même d’un astéroïde.
Vous serez en mesure de déterminer la forme de son orbite et d’observer comment la deuxième loi de Kepler s’applique.
Contrôles :
Curseur pour l’excentricité
Cette barre de défilement contrôle la forme de l’orbite elliptique de l’objet, en déterminant ce qu’on appelle l’ « excentricité » de l’ellipse.
Plus le nombre est grand, plus l’ellipse sera « aplatie ». Un cercle parfait a une excentricité de 0, même si aucun objet réel n’a une orbite parfaitement circulaire.
Une excentricité de 1 nous donnerait une parabole plutôt qu’une ellipse, alors nous ne l’avons pas incluse. En réalité, c’est très rare que les orbites des objets se
rendent près d’une excentricité de 1.
Nous avons limité l’excentricité dans ce diagramme à 0,95, car l’orbite deviendrait trop aplatie avec des valeurs plus grandes que ça.
Curseur pour le jour de l’année
Cette barre de défilement change le jour de l’année, permettant de déplacer l’objet dans son orbite autour du Soleil.
Case à cocher pour l’excentricité de la Terre
Si vous cochez cette case, le diagramme va vous montrer une orbite équivalente à l’excentricité de la Terre. (Celle-ci est de 0,01671.)
Vous verrez que ça ressemble presque à un cercle. La plupart des diagrammes doivent exagérer l’excentricité orbitale pour pouvoir vous montrer le concept des « aires égales »
(comme nous avons dû le faire!). Dans l’univers réel, l’orbite de la Terre est quasiment circulaire, et le concept serait presque impossible à montrer.
Ici, avec un diagramme qui correspond à l’orbite réelle de la Terre, vous pouvez voir qu’il n’y a pas beaucoup de variation dans la vitesse de la Terre d’un jour à l’autre,
ni dans la distance entre la Terre et le Soleil. C’est une bonne chose. Cela veut dire que la distance orbitale et les changements de vitesse sont suffisants pour permettre
de rendre les choses intéressantes – sans rendre les choses trop dangereuses sur la Terre si jamais on se rapproche trop du Soleil!
Lois du mouvement de Kepler
Les lois de Kepler étaient impressionnantes étant donné qu’elles ont été mises en place au début du 17e siècle. Elles ont clarifié la théorie de Copernic, et brillent aussi par leur simplicité.
Première loi de Kepler
Celle-ci est la plus simple. Elle affirme que les objets orbitent dans des trajectoires en forme d’ellipses plutôt qu’en forme de cercles.
Elle dit aussi que le Soleil occupe un des foyers de l’ellipse plutôt que d’en être le centre. Il faudrait vous en expliquer plus à propos des mathématiques des ellipses pour vous
expliquer ce qu’est exactement un foyer. Pour l’instant, nous pouvons vous dire que si une orbite était un cercle parfait, alors le Soleil en occuperait le centre.
Plus l’ovale est aplati, plus loin du centre le Soleil sera. Vous pouvez voir cela dans le diagramme.
Troisième loi de Kepler
Expliquons maintenant la troisième loi de Kepler, vu qu’elle est assez simple. Cette loi dit que si on sait combien de temps cela prend pour que quelque chose fasse le
tour du Soleil, alors on saura à quelle distance du Soleil cet objet doit être (ou vice-versa). Ça semble assez évident, mais ça a beaucoup impressionné Kepler quand il
a découvert ce principe. Nous allons utiliser cette loi dans un ensemble futur de diagrammes à propos des orbites. Pour l’instant, il suffit de savoir qu’il y a une relation
simple entre la période de révolution d’une orbite et son rayon.
Deuxième loi de Kepler
La deuxième loi est la moins évidente des trois, mais est aussi importante. Elle affirme que des aires égales sont balayées dans des temps égaux.
C’est plus facile à expliquer en vous le montrant dans le diagramme. Si vous déterminez une excentricité pour l’orbite elliptique, vous verrez une partie verte qui relie la planète au Soleil. Cette partie a un peu la forme d’un triangle. Maintenant, si vous changez le jour de l’année, la planète va se déplacer dans son orbite et la partie verte va suivre la planète. Même si la distance entre la planète et le Soleil change, et que le triangle vert passe de court et large à long et mince, l’aire de la partie verte demeure toujours la même.
Cela ne semble pas très important. Après tout, qui s’intéresse à une aire invisible dans l’espace? C’est toutefois important à cause d’une conséquence directe de cette loi : si vous réglez l’excentricité à un nombre assez élevé (peut-être autour de 0,80), alors vous verrez que quand la planète est proche du Soleil (lorsqu’elle est à la « droite » du Soleil dans le diagramme), la distance parcourue dans l’orbite en un seul jour est assez grande. Du moins, c’est une grande distance comparée à la distance parcourue en un jour quand la planète est loin du Soleil (à la « gauche »). Ce mouvement quotidien est la partie de la circonférence de l’ellipse recouverte par le triangle vert, donc la longueur de la base du triangle. (ce n’est pas la même chose que le nombre écrit à côté de la distance dans la légende : cette distance est plutôt celle entre l’objet et le Soleil pour ce jour-là!))
Vu que la distance parcourue quotidiennement dans l’orbite d’un objet change pendant son parcours, cela veut dire que la vitesse de la planète change! Quand la planète est à son point le plus proche du Soleil (un point appelé « périhélie »), elle se déplace plus rapidement qu’elle ne le fera jamais dans son orbite. Quand la planète est à son point le plus éloigné (un point appelé « aphélie »), elle se déplace à sa vitesse la plus lente. C’est un fait très important, et grâce à la troisième loi, on peut obtenir des données très précises à propos d’une orbite en utilisant des mathématiques très simples.
Utiliser les barres de défilement
Quand vous réglez l’excentricité, vous pouvez voir que l’aire du triangle vert va changer (selon la deuxième loi). Vous pouvez voir la valeur de cette aire dans la légende.
Cette aire ne changera plus, sauf si vous changez l’excentricité – donc la forme de l’orbite.
Si vous changez ensuite le jour de l’année, la vitesse de la planète va changer alors qu’elle se déplace dans son orbite elliptique. Si vous réglez l’excentricité à 0 (donc une orbite circulaire), alors la vitesse ne changera jamais pendant l’année. Mais rappelez-vous, ceci n’arrive pas dans le vrai univers. Plus l’orbite est aplatie, plus il y aura une grande différence de vitesse entre l’aphélie et la périhélie.
Vous pourriez aussi vous demander pourquoi on a déterminé que la durée de l’ « année » de la planète serait de 365 jours. Selon la troisième loi, on sait que si la distance moyenne entre la planète et le soleil est de 1 AU, alors l’année contiendra 365 jours. Nous avons créé ces ellipses pour que la distance moyenne demeure constante pour des ellipses de n’importe quelle excentricité, et cela nous donne donc le même nombre de jours dans une année!
Ce que vous pouvez apprendre :
- Vous pouvez voir comment l’excentricité influence la forme d’une orbite planétaire elliptique.
- Vous pouvez voir comment les lois de Kepler déterminent les distances orbitales tout comme les « aires égales dans des temps égaux ».
- Vous pouvez voir comment la vitesse orbitale d’un objet change pendant son parcours dans son orbite.
- Vous pouvez apprendre les termes « périhélie » et « aphélie ».
Conjonction et opposition
Voyez les mouvements des planètes internes et externes par rapport à la Terre.
Consultez les instructions du diagramme 19Refermer les instructions
Diagramme 19 :
Conjonction et opposition
Ce que vous regardez :
Voici une vue à vol d’oiseau de l’orbite de la Terre et d’une autre planète autour du Soleil. Vous pouvez choisir entre utiliser la planète rouge-orange comme planète interne (comme Mercure ou Vénus) ou comme planète externe (comme Mars), et voir comment elle se déplace par rapport à la Terre alors qu’elles orbitent toutes les deux autour du Soleil.
Nous avons compressé l’ensemble du zodiaque et l’avons placé dans une bannière au sommet du diagramme, pour que vous puissiez voir les mouvements apparents du Soleil et de la planète alors que le temps passe. Pour les planètes internes, nous avons gardé le Soleil en position fixe pour vous aider à voir les événements importants survenant dans l’orbite de la planète interne. Pour les planètes externes, nous conservons les étoiles en position fixe pour laisser le Soleil et les planètes externes se déplacer à travers le zodiaque comme ils le font normalement (comme vu depuis la Terre).
Contrôles :
Menu déroulant pour planète « interne » ou « externe »
Ce menu déroulant vous permet d’alterner entre avoir la planète rouge-orange plus près du Soleil que la Terre (appelée une « planète interne »),
ou plus loin du Soleil que la Terre l’est (appelée une « planète externe »). Nous avons deux images différentes pour ça car la terminologie utilisée par les
astronomes change selon le type de planète.
Curseur pour la période orbitale de la planète
Ce curseur change la distance entre la planète rouge-orange et le Soleil. Selon la troisième loi de Kepler, cela change donc le nombre de jours que prend la Terre pour faire son orbite autour du Soleil.
Curseur pour la vitesse
Tout comme pour les autres curseurs pour la vitesse, celui-ci vous permet d’observer la Terre et les autres planètes effectuer leur orbite autour du Soleil.
Vous pouvez déplacer le curseur vers la droite pour voir la planète orbiter dans la bonne direction, ou le déplacer vers la gauche si vous avez manqué quelque chose et
voulez brièvement retourner en arrière pour l’observer de nouveau.
Ce qu’on doit observer
Voici quelques événements que vous pouvez observer dans la bannière au sommet du cadre du diagramme :
Planètes internes
Vous verrez que dans tous les cas, la planète interne se déplace autour du Soleil plus vite que ne le fait la Terre. Aussi, la planète interne reste toujours
relativement proche du Soleil quand on l’observe depuis la Terre; même si son orbite est vraiment proche de celle de la Terre (ce qui ne serait pas possible dans
la vraie vie, car cela rendrait les orbites des planètes instables), la planète interne ne peut jamais être éloignée à plus de 90° du Soleil. Généralement, c’est même beaucoup moins que ça.
Élongations
Quand la planète interne se rend aussi loin du Soleil que possible, vous verrez apparaître dans la bannière en haut un encadré qui dit « Plus grande élongation [est ou ouest] ».
Ceci veut dire exactement ce à quoi ça ressemble – le plus loin possible du Soleil que la planète peut être. Si la planète se retrouve du côté « droit » du Soleil,
il s’agit d’une élongation ouest. La planète sera alors visible dans le ciel le matin car elle se lève avant le Soleil. Si elle est du côté « gauche » du Soleil, il s’agit d’une élongation est.
La planète sera visible dans le ciel après le coucher du Soleil. (On le sait, ça sonne contradictoire. Les élongations sont nommées selon leur position relative au Soleil –
et si un objet est à l’Ouest du Soleil dans le ciel, il va se lever et se coucher en premier. C’est comme ça que ça fonctionne!)
Nous avons choisi de garder le Soleil au centre de la bannière située en haut, car cela représente le point médian entre les deux élongations.
Conjonctions
Il y a aussi deux situations où la Terre, le Soleil et la planète interne sont alignés en ligne droite. Ces situations sont appelées « conjonctions », car la planète interne et le Soleil nous apparaissent
dans la même partie du ciel. Si vous utilisez le curseur pour garder les planètes en mouvement, vous allez voir cette situation survenir éventuellement. Si vous gardez le tout en mouvement suffisamment longtemps,
vous verrez que cet alignement peut survenir de deux façons : soit que la planète interne est entre la Terre et le Soleil, ou elle se retrouve de l’autre côté du Soleil. Dans le premier cas,
c’est ce qu’on appelle une « conjonction inférieure ». Dans l’autre cas, il s’agit d’une « conjonction supérieure ».
Vous pouvez vous rappeler qu’ « inférieur » représente moins que « supérieur » et que dans une conjonction inférieure, la distance entre la planète interne et la Terre est plus petite que pendant une conjonction supérieure.
Transits
On doit mentionner que lors d’une conjonction supérieure, la planète interne ne sera jamais visible; elle sera cachée par la lumière écrasante du Soleil. Mais avec le diagramme, il semble qu’on serait capable
de voir la planète interne lors de la conjonction inférieure. La planète semble pouvoir se déplacer à travers la face du Soleil, et on pourrait utiliser des lunettes à éclipses ou des filtres solaires pour pouvoir la voir.
Mais rappelez-vous, on a dit qu’on a aplati le zodiaque pour pouvoir vous le montrer dans la bande en haut du diagramme. Dans la vraie vie, quasiment à toutes les fois qu’il y a une conjonction inférieure,
la planète semble être « au-dessus » ou « en-dessous » du Soleil dans l’écliptique, alors elle ne sera pas visible.
C’est similaire à ce qui se passe avec la Lune, ce qui fait qu’on n’a pas d’éclipse à tous les mois.
Il y a en fait des moments où Mercure ou Venus vont apparaître en train de passer devant le Soleil. Ces événements sont appelés « transits » et ils sont assez rares. (Pour Vénus, ils sont TRÈS rares). Les prochains transits de Mercure vont survenir en 2032 et 2039 et le prochain pour Vénus n’arrivera pas avant 2117. Inscrivez ces dates à votre calendrier!
Planètes externes
Comme on l’a dit plus tôt, les planètes externes ont aussi des moments importants qui surviennent lors de leurs orbites. Cette fois, il y en a quatre :
Quadrature
Les planètes externes n’ont pas d’ « élongations », parce qu’elles peuvent apparaître n’importe où dans le ciel par rapport au Soleil. Les astronomes ont un terme pour le moment où elles apparaissent
exactement à 90° du Soleil : « quadrature ». Comme avec l’élongation, il y a une quadrature occidentale et une orientale – mais rien de bien spécial ne se passe ici. Quand cela survient dans le diagramme,
vous verrez un encadré dans la bannière en haut pour décrire ce qui se passe.
Conjonction
Rappelez-vous que « conjonction » veut dire que la planète et le Soleil sont au même endroit dans le ciel. Comme pour les planètes internes, vous ne pourrez pas voir une planète externe quand il y a une conjonction : le Soleil est trop brillant!
Opposition
Le moment le plus excitant dans l’orbite d’une planète externe est quand elle se retrouve dans son « opposition ». Cela veut dire qu’elle est exactement à l’opposé du Soleil dans le ciel.
Ça tend à être observable pendant toute la nuit. Mais encore mieux que ça – la planète sera à son point le plus proche de la Terre à ce moment-là aussi. Elle apparaît plus grande qu'elle ne peut
jamais l'être depuis la Terre. Cette combinaison où on a toute la nuit pour observer et d’avoir une planète qui semble aussi grosse qu’elle peut l’être est très importante.
Mars en est le meilleur exemple, parce que la différence entre son apparition à l’opposition et à la conjonction (ou bien ce qui ce serait à la conjonction!) est stupéfiante. Au moment où Mars brille le plus,
elle peut apparaître comme étant encore plus brillante que Sirius (étant alors quasiment aussi brillante qu’une magnitude de -3!). À l'opposé, à son moment le moins brillant, Mars aurait une magnitude de +1,8.
Mars apparaîtra comme étant quasiment huit fois plus large à son opposition qu’à sa conjonction.
C’est vrai qu’à l’œil nu, Mars ne semblera jamais plus grosse qu’un point de lumière dans le ciel. Il est aussi vrai que Vénus, à son moment le moins brillant, sera légèrement plus brillante que Mars et ce, de beaucoup. Mais si d’observer Mars est sur votre liste de choses à faire, il est mieux de choisir un moment où elle est à son opposition. Et même si nous n’avons pas montré l’excentricité de l’orbite de Mars, il y en a certainement une. Cela veut dire aussi qu’il est mieux de choisir une opposition qui a lieu près de la périhélie de Mars. Les oppositions surviennent à peu près tous les deux ans, et la prochaine opposition près de la périhélie aura lieu en 2035.
Mouvement rétrograde
C’est plus facile à voir sur le diagramme, mais en voici une description :
Normalement, toutes les planètes semblent se déplacer d’ouest en est à travers le ciel. (Donc de la « droite » vers la « gauche » dans l’hémisphère nord, et de la « gauche » vers la « droite » dans l’hémisphère sud.) La Terre se déplace plus vite dans son orbite que n’importe quelle planète externe. Quand il y a une opposition, la Terre a alors rattrapé cette planète. Alors que la Terre dépasse cette planète externe, pendant un certain temps (aussi long que quelques mois!), la planète semble se déplacer à reculons contre le décor formé d’étoiles. Une fois que la Terre l’a dépassée et a poursuivi son chemin, la planète semblera de nouveau se déplacer dans la bonne direction. C’est un peu comme quand vous êtes à bord d’une voiture qui se déplace plus vite que la voiture à côté de vous. Quand vous la dépassez, l’autre voiture semble aller de reculons.
Cette illusion d’optique s’explique facilement par le modèle de Copernic concernant les planètes qui tournent autour du Soleil. Avant que ce modèle ne soit accepté, les explications étaient par contre très difficiles. Les scientifiques de l’ancien temps ont dû inventer toutes sortes de théories tordues pour essayer de comprendre ce qui se passait. Vous pouvez lire par vous-même à propos d’une de ces théories appelée « épicycles ».
Ce que vous pouvez apprendre :
- Vous pouvez apprendre les termes concernant l’emplacement des moments importants dans les orbites des planètes, comme ils apparaissent depuis la Terre.
- Vous pouvez voir comment les transits surviennent.
- Vous pouvez voir pourquoi Mercure et Vénus ne semblent jamais parcourir plus d’une certaine distance par rapport au Soleil dans le ciel.
- Vous pouvez voir pourquoi il est mieux d’observer les planètes externes pendant leur « opposition ».
- Vous pouvez apprendre à propos du mouvement rétrograde et pourquoi il est observé avec toutes les planètes externes.
L’équation du temps
Une introduction à l'équation du temps et au cadran solaire.
Consultez les instructions du diagramme 20Refermer les instructions
Diagramme 20 :
L’équation du temps
Ce que vous regardez :
Il y a trois graphiques dans ce diagramme. Les deux premiers montrent les composantes principales de ce que les astronomes appellent l’ « équation du temps ». Le troisième graphique est le résultat qu’on obtient quand on met les deux premiers ensemble (prenez en note, les temps qui sont montrés ne s’additionnent peut-être pas parfaitement vu qu’on les a arrondis).
Expliquons ce que ces graphiques veulent dire. Voici tout d’abord une mise en contexte :
Qu’est-ce que l’équation du temps?
Commençons en réfléchissant à comment vous pourriez mesurer le temps pendant le jour, en utilisant seulement le Soleil. Vous ne pouvez pas
voir les étoiles et vous n’avez ni pendule, ni sablier, ni bougies, même pas de l’eau qui s’égoutte par un petit trou.
Votre téléphone est déchargé et vous n’avez certainement pas une montre ou une horloge de secours!
Le cadran solaire
Vous pourriez décider que le moyen le plus facile de mesurer le temps serait de placer un bâton dans le sol et d’observer l’ombre du Soleil se
déplacer sur le sol au fur et à mesure que le jour avance. (C’est certainement plus facile que de fabriquer une montre de poche!)
Bien sûr, vous devez vous assurer que le bâton est parfaitement droit de haut en bas, ce que vous pouvez faire avec un fil à plomb.
Il s’agit d’une des plus anciennes méthodes de calcul du temps. Elle se rapproche beaucoup de ce qu’on appellerait le « vrai » temps. Le bâton dans le sol projette une ombre qui dépend de l’altitude et de l’azimut du Soleil – c’est-à-dire à quelle hauteur il se trouve dans le ciel et à quelle distance il se trouve de l’est et de l’ouest de l’horizon. Alors que le Soleil est de plus en plus haut dans le ciel, l’ombre du bâton est de plus en plus courte. Alors que le Soleil se déplace à travers le ciel d’est en ouest, l’ombre semble se déplacer de l’ouest vers l’est. Les cadrans solaires sont conçus pour que l’angle entre l’ombre et le vrai nord/sud vous permette de savoir l’heure qu’il est.
Problèmes avec le cadran solaire
Bien sûr, le cadran solaire fonctionne seulement pendant le jour, mais on peut utiliser d’autres méthodes la nuit pour nous situer.
Le jour suivant, on peut alors tout recalibrer une fois qu’on est en mesure d’utiliser de nouveau le cadran solaire.
Le cadran solaire rencontre aussi des problèmes quand le temps est nuageux. Encore une fois, on devrait alors compter sur des méthodes alternatives pour gérer nos vies quotidiennes. S’il fait nuageux pendant quelques jours de suite, nos méthodes alternatives pourraient se retrouver désynchronisées par rapport au cadran solaire.
Le cadran solaire doit aussi être calibré pour votre latitude et le moment de l’année. L’angle que l’ombre du Soleil fait sur le sol change avec ces deux facteurs, alors vous devez donc avoir une norme connue à laquelle « régler » votre cadran solaire.
Le temps solaire dépend aussi grandement de votre longitude. À l’équateur, les gens qui sont situés à environ 28km à l’est ou à l’ouest l’un de l’autre vont voir leur heure solaire locale différer d’une minute complète! Ce n’est pas un problème si la précision de votre usage du temps se limite à « milieu d’avant-midi » ou « fin d’après-midi ». Mais cela devient plus compliqué si vous essayez d’établir un horaire de train qui est précis à la minute près. Si vous avez besoin de précision à la seconde près, vous avez vraiment besoin d’une norme plus fiable que le Soleil.
Même avec tous ces problèmes, le cadran solaire est quand même une invention assez remarquable – étant donné qu’il s’agit seulement d’un bâton planté dans le sol. C’est un moyen sans grande technologie qui permet de se rapprocher étonnamment de l’heure exacte.
La vitesse du Soleil n’est pas constante
Alors que des normes plus précises étaient comparées au cadran solaire, les gens ont remarqué qu’il y avait des erreurs avec le cadran solaire qui ne
pouvaient pas s’expliquer facilement. L’ombre du Soleil pouvait être comparée avec d’autres méthodes pour compter le temps, et on s’est rendu compte
que le cadran solaire ne mesurait pas le temps de façon uniforme d’un jour à l’autre. Même en prenant en compte tous les correctifs auxquels les gens
pouvaient penser, il y avait certains moment de l’année où l’ombre se retrouvait en avant ou en arrière d’où elle aurait dû se trouver. Le Soleil se
retrouvait à atteindre son point le plus élevé dans le ciel un peu plus tôt ou plus tard qu’il aurait dû, et on n’arrivait tout simplement à expliquer ça.
L’erreur pouvait être presque de zéro, ou bien il pouvait y avoir jusqu’à un quart d’heure d’avance ou de retard.
Le Soleil atteignait son point le plus haut dans le ciel à différentes heures à chaque jour!
Les mesures n’étaient pas non plus une erreur – car le même phénomène se reproduisait partout où le cadran solaire était utilisé. De plus, le même scénario se répétait encore et encore, année après année. Rendu à la mi-février, le Soleil était toujours en retard par rapport à où il aurait dû se trouver. Au début de novembre, il était très en avance, alors qu’à la mi-avril, il était quasiment parfaitement synchronisé. Très étrange!
Bien sûr, il n’y avait pas moyen d’expliquer cela en utiliser les mathématiques ou la physique de l’ancien temps. C’était ce que c’était, alors c’était tout simplement accepté comme étant la manière avec laquelle l’univers fonctionnait. Vu que ce phénomène se répétait, les hommes de l’ancien temps l’ont consciencieusement modélisé et l’ont inclus dans leur calcul du temps chaque fois qu’un cadran solaire était utilisé.
L’équation du temps
Aujourd’hui, on appelle « équation du temps » cet écart entre où le Soleil devrait se trouver et où il se trouve vraiment. (Dans ce cas, le mot « équation »
signifie davantage que nous équilibrons le fait que le Soleil soit rapide ou lent, plutôt que d’essayer de résoudre une équation mathématique où deux
termes sont égaux.) De plus, dans cette ère moderne, on a suffisamment de connaissances pour être capable de comprendre et d’expliquer ce phénomène.
Rappelez-vous qu’on a déjà appris quelques notions à propos de l’orbite de la Terre; tout d’abord, elle a une obliquité (diagramme 13) et une excentricité
(diagramme 18). On doit maintenant tenir compte de ces deux effets séparément, alors dans la discussion qui suit, nous allons tenir compte de
quatre « Soleils » différents :
- Un Soleil « Moyen », soit le Soleil auquel on s’attend – celui qui se déplace exactement à la même vitesse à travers le ciel à n’importe quel moment de l’année.
- Le Soleil « Exc », qui est un Soleil imaginaire qui se déplace en relation avec le Soleil Moyen avec les effets de l’excentricité seulement,
- Le Soleil « Obl », qui est aussi un Soleil imaginaire qui se déplace en relation avec le Soleil Moyen avec les effets de l’obliquité seulement,
- Finalement, le Soleil « Réel », qui est le Soleil qu’on voit vraiment dans le ciel, et qui se déplace plus lentement ou plus rapidement que le Soleil Moyen. Il s’agit d’une combinaison du Soleil Exc et du Soleil Obl.
Tout ceci fera plus de sens lorsqu’on expliquera chacun des graphiques.
Pourquoi avons-nous besoin de tous ces Soleils? Et bien, on a besoin du Soleil Moyen pour servir de base de référence aux autres. On a besoin du Soleil Réel pour parler du Soleil qu’on voit réellement dans le ciel. Ensuite, on a besoin des faux « Soleils » qui décrivent séparément les effets de l’excentricité et de l’obliquité de l’orbite de la Terre. À la fin, on combine le Soleil Exc et le Soleil Obl pour obtenir le Soleil Réel.
Il est très important de se rappeler que le Soleil Exc et le Soleil Obl ne sont pas le vrai Soleil qu’on voit dans le ciel. Aussi, ils ne sont pas pareils l’un et l’autre. Le Soleil Moyen dont on se sert dans tous les diagrammes reste toujours le même, par contre.
Comme on l’a indiqué, il y a deux facteurs principaux qui composent l’équation du temps :
Excentricité
On a appris dans le diagramme 18 que l’orbite de la Terre est elliptique plutôt que d’être circulaire. Ça veut dire qu’à certains moments de l’année,
la Terre se déplace plus vite ou plus lentement qu’à d’autres moments. Parce que les mouvements apparents du Soleil à travers le zodiaque sont causés par
les mouvements réels de la Terre dans son orbite, ça veut dire qu’on voit le Soleil qui semble ralentir ou accélérer un peu à différents moments de l’année.
Il est vrai que la précession entraîne un déplacement ou un décalage de ces périodes de l’année, mais seulement sur de très longues périodes. On peut affirmer sans se tromper qu’à ce stade-ci de l’histoire, le Soleil semble se déplacer dans le ciel plus rapidement en janvier qu’en juillet. Ce changement de vitesse amène une différence entre l’endroit où nous observons le Soleil, et l’endroit où il serait s’il se déplaçait à une vitesse constante.
On peut calculer et représenter graphiquement cette différence en établissant un Soleil Moyen comme étant la norme, et en déterminant à quel point le Soleil Exc sera loin en arrière ou en avant (en se basant seulement sur les effets de l’excentricité de l’orbite de la Terre). Lorsque nous faisons ça, nous obtenons le premier graphique que vous pouvez voir dans le diagramme.
Pour pouvoir lire ce graphique, vous pouvez régler le jour de l’année à la date de votre choix. Alors que vous changerez la date, le Soleil Moyen va se déplacer vers le haut ou vers le bas au milieu du graphique, alors que le Soleil Exc va se déplacer autour. Si le Soleil Exc est à la gauche du Soleil Moyen pour un jour donné, ça veut dire que le Soleil Exc est plus lent qu’il ne devrait l’être ce jour-là. En d’autres mots, le midi réel survient avant que le Soleil Réel n’atteigne dans les faits son point le plus haut dans le ciel. Si le Soleil Exc est à la droite du Soleil Moyen, alors le Soleil Exc est en avance de l’endroit où il devrait être, et midi va survenir après que le Soleil Réel ait atteint son point culminant pour la journée.
Si les deux Soleils sont au même endroit (comme ils le sont autour du 3 janvier et du 5 juillet), alors ce sont les jours où tout s’équilibre, et cet ajustement provoqué par l’excentricité n'apporte rien à l'équation du temps.
Vous pouvez lire la légende au bas du graphique pour voir quelle avance ou quel retard le Soleil Exc a pour un jour donné.
(NOTE : Si vous êtes dans une classe de mathématiques avancées, vous verrez que le graphique ressemble à une onde sinusoïdale, avec une période d’exactement une année. À la base, c’est ce que c’est, et si vous l’avez modélisé avec une équation de trigonométrie standard, vous serez très proche des valeurs réelles que nous observons! La période est d’un an, parce qu’au cours d’une année, la Terre se déplace depuis son point le plus proche du Soleil (périhélie) à son point le plus éloigné du Soleil (aphélie), et puis elle fait le trajet inverse – traçant le contour d’une onde sinusoïdale parfaite. Ça fait en sorte que sa vitesse établit un modèle de « plus vite, puis plus lent » une fois pendant l’année.)
Obliquité
Celui-ci est un peu plus difficile à expliquer, mais son effet est tout aussi important. On sait que le Soleil ne suit pas une trajectoire droite dans le ciel pendant
le cours d’une année. Sa trajectoire est courbée, alors sa déclinaison est élevée en juin, et basse en décembre. On a illustré ceci dans le diagramme 13.
(Pour la discussion qui suit, nous allons ignorer les effets de l’excentricité, dans le but de se concentrer seulement sur l’obliquité.)
L’obliquité de l’orbite de la Terre est ce qui amène l’écliptique à se lever au-dessus et ensuite à retomber en-dessous de l’équateur céleste. Le Soleil voyage alors dans une trajectoire courbe qui ressemble à une onde sinusoïdale. (Dans le but de simplifier les choses, on a aplati cette onde dans le diagramme 19, mais vous pouvez très bien la voir dans le diagramme 13.) Ce mouvement de haut en bas du Soleil amène sa déclinaison à changer pendant le cours d’une année. Comme on l’a vu dans le diagramme 1, le Soleil peut être à l’extrême nord en déclinaison (comme en juin et juillet), à l’extrême sud (comme en décembre et janvier) ou directement à l'équateur (aux équinoxes vernal et automnal). Tout ceci est dû à l’obliquité de l’orbite de la Terre.
Vu que le Soleil se déplace à une vitesse constante le long de la courbe de son parcours à travers les étoiles (ce qui est une onde sinusoïdale), mais que le Soleil Moyen se déplace seulement sur la ligne droite formant l’axe de cette trajectoire (la ligne médiane de l’onde sinusoïdale), cela fait du sens que le Soleil Obl se déplace plus rapidement horizontalement que le Soleil moyen quand il est au haut ou au bas de la trajectoire de cette onde sinusoïdale. Ce sont les deux moments de l’année où ses mouvements sont les plus parallèles aux déplacements en ligne droite du Soleil Obl. Chaque fois que le Soleil se déplace selon un angle par rapport à cette ligne médiane (ce qui arrive aussi deux fois par année), il se déplacera plus lentement horizontalement que le Soleil Moyen à travers le ciel.
[Encore une fois, pour ceux qui sont dans des classes avancées de mathématiques ou de science physique (parce qu’il n’y a pas de moyen « facile » pour décrire ceci), on peut affirmer que la composante de la vélocité du soleil obl le long de la trajectoire du Soleil moyen est la plus grande lorsque le vecteur vitesse du Soleil obl est le plus parallèle à la trajectoire du Soleil moyen. Ces points se trouvent au maximum et au minimum du graphique sinusoïdal qui représente l’écliptique par rapport à l’équateur céleste. Cette composante horizontale de la vélocité est au moins présente les deux fois par an où le Soleil traverse l’équateur selon un certain angle.]
Peu importe comment vous le dites, ça veut dire qu’il y a deux moments dans l’année où le Soleil Obl se déplace plus vite que le Soleil Moyen. Si nous traçons l’emplacement du Soleil Obl (qu’il soit devant ou derrière le Soleil Moyen) pour l’année entière, nous obtenons le graphique dans le milieu du diagramme.
Parce qu’une année contient deux cycles de ce mouvement lent-rapide-lent du Soleil Obl, on peut voir que l’onde sinusoïdale pour l’obliquité a deux périodes pendant le cours d’une seule année. Encore une fois, vous pouvez modéliser ce graphique avec une équation de trigonométrie standard et arriver assez proche des valeurs observées.
À travers tout ceci, on doit vous le rappeler encore une fois : les Soleils Obl et Exc ne sont pas les mêmes. Leurs effets ont dû être séparés et isolés pour pouvoir obtenir des résultats aussi nets que ceux-ci.
Résultat
Le graphique « Résultat » est ce qu’on obtient si on additionne ensemble le graphique de l’excentricité et celui de l’obliquité pour chaque jour de l’année.
Ça représente le Soleil « réel » - celui qu’on voit vraiment dans le ciel.
La forme est étrange, mais ce n’est rien de plus que la somme combinée des deux ondes sinusoïdales qu’on a vues pour l’excentricité et l’obliquité.
Par exemple, le 2 juillet, on voit que le Soleil Exc est 23 secondes en retard par rapport à où il devrait être. Le Soleil Obl est en retard de 3m32s. Ça veut dire qu’il y a un retard total de 3m 55s. En raison d’une erreur d'arrondissement, le graphique résultat nous montre plutôt un retard total de 3m56s. Alors, le Soleil Réel est 3m 56s en arrière d’où il devrait être s'il se déplaçait à la même vitesse tout le temps. Dit d’une autre manière, quand le cadran solaire indique midi un 2 juillet, il est en fait 12h03m56s.
Nous utiliserons ce graphique Résultat à bon escient dans le prochain diagramme!
Rappelez-vous, le vrai Soleil qu’on voit dans le ciel est le Soleil Réel, et non pas le Soleil Obl ou le Soleil Exc. Le Soleil Réel est la combinaison des deux.
Le cadran solaire revisité
Il s’avère que si vous faites un tableau indiquant dans quelle mesure ces deux facteurs contribuent à ce que le Soleil Réel soit plus rapide ou plus lent que le
Soleil Moyen, et que vous les additionnez, vous obtiendrez un graphique indiquant exactement l’ajustement à apporter à l’ombre de votre cadran solaire pour chaque jour de l’année.
Si vous faites ça, et mesurer avec suffisamment de précaution, alors le cadran solaire sera très précis. Si vous faites ensuite les bons ajustements pour la longitude
et la latitude, vous pourriez alors effectivement utiliser le cadran solaire pour dire l'heure de manière assez précise pour votre vie de tous les jours.
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Jour de l’année
Cette commande nous déplace à travers chaque jour de l’année. Vous pouvez utiliser le curseur ou encore utiliser les flèches de droite et de gauche de votre clavier pour changer la date.
Alors que vous déplacez le curseur, le Soleil réel et le Soleil moyen vont se déplacer à travers les graphiques et tracer les composantes de l’équation du temps.
Veuillez prendre en note qu’alors que le Soleil se déplace vers le bas dans chaque graphique, il avance dans le temps.
Vitesse du jour de l’année
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes. Elle vous permet de déplacer les objets dans les diagrammes à des vitesses variables.
Cliquez et maintenez le curseur enfoncé.
Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement. Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Cette barre de défilement contrôle le jour de l’année. Elle déplace les Soleils réels et moyen à travers les jours de l’année, ce qui les amène à tracer les composantes de l’équation du temps.
Choses à remarquer
Vous verrez qu’il y a quatre moments de l’année où les Soleils Moyen et Réel sont quasiment à la même place dans le graphique résultat. Ça veut dire que pour ces jours-là,
il n’y a pas d’ajustement de l’équation du temps, et vous cadran solaire indiquera la bonne heure solaire locale.
Vous remarquerez aussi que le graphique résultat présente deux grands écarts par rapport à la ligne médiane du Soleil Moyen, et deux petits écarts par rapport à celle-ci. Si vous regardez de près, vous verrez que le grand écart à la droite en novembre est plus grand que le petit écart à la gauche en février. Vous verrez aussi que le petit écart à la droite en mai est plus petit que le petit écart à gauche en juillet/août. Ces faits seront d’intérêt pour nous dans le prochain diagramme.
Quelques informations supplémentaires
Pour ceux d’entre vous qui ont une formation musicale, vous remarquerez que le graphique résultat commence à ressembler à ce que vous pourriez voir dans un oscilloscope quand un son
musical est joué. Chaque tonalité musicale a une forme d’onde particulière, que nous entendons comme étant différentes caractéristiques sonores (appelées « timbres »),
ce qui nous permet d’identifier différents instruments de musique jouant à la même hauteur. Les formes de ces ondes peuvent être très simples ou très compliquées, mais elles sont
toutes le résultat de l’addition des combinaisons de fréquences des composantes telles que les graphiques d’excentricité et d’obliquité.
Lorsque vous entendez une tonalité musicale très plaisante, vous pouvez être certain que plusieurs fréquences ont été additionnées ensemble pour obtenir son modèle d'ondes. Si tout ce que vous aviez à regarder était ce résultat composé de ce modèle, il pourrait sembler impossible de déterminer toutes les ondes composantes qui se sont combinées pour le constituer. En fait, c’est très difficile, mais pas impossible! Merci au travail d’un mathématicien appelé Joseph Fourier, on peut décomposer n’importe quel modèle d’onde périodique complexe en ses composantes sinusoïdales, et voir comment les différentes parties se combinent pour créer les sons des différents instruments qu’on connaît. C’est en fait ainsi que sont créés les échantillons faits par ordinateur pour la musique électronique.
Il est impressionnant qu’on puisse ainsi observer des modèles qui s’appliquent à des sujets aussi différents que l’astronomie et la musique, et les analyser ensuite ensemble en utilisant les mêmes mathématiques!
Ce que vous pouvez apprendre :
- Vous pouvez voir pourquoi vous devez ajuster l’heure que vous voyez sur un cadran solaire pour pouvoir obtenir la bonne heure locale – sauf pour quatre jours dans l’année!
- Vous pouvez voir comment l’équation du temps est le résultat naturel des mouvements orbitaux de la Terre.
- Vous pouvez voir un exemple simple de comment plusieurs effets peuvent s’additionner pour créer un résultat.
- Vous pouvez voir un exemple tiré de la vraie vie de l’utilisation des graphiques d’ondes sinusoïdales que vous avez appris dans les cours de trigonométrie!
L’analemme
La trajectoire annuelle apparente du Soleil dans le ciel.
Consultez les instructions du diagramme 21Refermer les instructions
Diagramme 21 :
L’analemme
Ce que vous regardez :
On a seulement deux graphiques dans ce diagramme. En premier, on a copié le graphique « Résultat » du diagramme 20 et on l’a mis à la gauche comme référence. On a ajouté le graphique à la droite pour vous montrer les mêmes données, mais d’une manière différente. Vous verrez sous peu comment on a fait ça.
Graphique de l’équation du temps – Deux manières différentes
On a déjà vu comment obtenir le graphique de l’équation du temps. Dans le diagramme 20, on a mis les jours de l’année sur l’axe des y,
puis on a pris la quantité de temps pour laquelle le Soleil était en « avance » ou en « retard » sur le cadran solaire et on a mis ça sur l’axe des x.
On sait que la déclinaison du Soleil se déplace pendant l’année, et qu’elle varie entre +23,5° et -23,5° car il s’agit de l’inclinaison de la Terre sur son axe. En fait, il est intéressant de tracer l’équation du temps non pas comme un graphique x-y, mais comme un graphique paramétrique.
Qu’est-ce qu’un graphique paramétrique?
Si vous n’avez pas étudié ça encore à l’école, vous pouvez penser que n’importe quel graphique paramétrique (pour nos objectifs dans cette discussion) est comme une figure que vous dessinez sur un morceau de papier sans lever votre crayon.
Vous pouvez utiliser des lignes droites ou des courbes autant que vous voulez, et vous pouvez les rendre aussi complexes que vous le désirez – avec des boucles partout.
Mais vous devez terminer où vous avez commencé pour que ce soit une trajectoire continue sans aucune coupure.
Vous avez aussi la permission d’aller plus vite ou plus lentement avec votre crayon autant que vous le voulez lorsque vous dessinez votre graphique. Ça veut dire que deux personnes pourraient avoir dessiné exactement la même figure, mais parce qu’une des deux personnes a été plus lentement que l’autre personne à un endroit et plus rapidement à un autre endroit, alors techniquement les graphiques paramétriques sont différents – même si la trajectoire tracée est exactement la même!
Si vous pensez à un insecte qui marche le long de la trajectoire que vous avez créée, alors l’insecte pourrait ramper très rapidement sur une partie de la courbe, puis ralentir pour faire une pause, ensuite effectuer un sprint jusqu'à la fin. Ce qui importe est que l’insecte ait rampé le long de la trajectoire que nous voulions, et qu’on puisse dire à quelle vitesse l’insecte rampait à n’importe quel point.
Quel est le rapport avec le Soleil?
Maintenant, regardez le graphique à la droite du diagramme. L’axe des x représente toujours les minutes, et il montre à quel point le Soleil est en avance ou en retard par
rapport au cadran solaire (tout comme précédemment). Mais maintenant, l’axe des y représente la déclinaison du Soleil au lieu de la date. En haut au sommet du graphique,
le Soleil est haut dans le ciel pour l’hémisphère nord, et au bas du graphique, il est haut dans le ciel pour l’hémisphère sud. En plein au milieu, il est au-dessus de
l’équateur avec une déclinaison de 0°.
Vous remarquerez aussi que nous avons mis des marques sur le graphique pour vous montrer le début de chaque mois de l’année. Il s’agit de la partie paramétrique du graphique, où nous vous montrons la vitesse à laquelle le Soleil se déplace le long de la courbe à chaque point. Il y a beaucoup plus de distance le long de la trajectoire entre octobre et novembre qu’il y en a entre juillet et août. C’est parce que le Soleil se déplace plus lentement à travers le ciel en juillet qu’en octobre – bien sûr, c’est parce que la Terre elle-même se déplace plus lentement dans son orbite en juillet! Tout concorde.
Qu’est-ce que ce graphique nous montre?
Si vous déplacez maintenant le curseur pour le jour de l’année, vous verrez que le graphique de l’équation du temps fait la même chose que dans le diagramme 20. Mais le graphique
à la droite va montrer le Soleil en train de parcourir une figure en forme de 8 dans une grande boucle, tout comme l’insecte dont on a parlé plus tôt, suivant la trajectoire encore et encore.
Le graphique nous montre où se trouve exactement le Soleil dans le ciel, pour chaque jour de l’année, exactement à midi sur votre horloge locale. Nous ne parlons pas de midi, heure solaire locale, mais bien de midi, heure locale moyenne, parce que le graphique tient déjà compte de l’avance ou du retard du Soleil.
Autrement dit, si votre horloge moderne dit qu’il est midi et que vous prenez en note l’endroit où le Soleil se trouve dans le ciel à ce moment, il serait au même endroit par rapport à son axe nord-sud indiqué dans le graphique.
C’est très important, alors on va le dire de nouveau : le graphique ne montre pas seulement l’avance ou retard que le Soleil a, mais il montre aussi à quelle hauteur dans le ciel il sera. C’est quelque chose que l’ancien graphique de l’équation du temps ne nous montrait pas du tout!
L’analemme
On a passé beaucoup de temps à parler du graphique sur la droite, alors on va lui donner un nom – c’est appelé un « analemme ». Ce mot a une étymologie difficile, mais à l’origine, il vient d’un mot racine qui veut dire « support » - comme dans le support ou la base d’un cadran solaire! Après tout, le maintien du temps avec un cadran solaire est une des raisons principales pour lesquelles l’analemme existe en premier lieu, alors ça fait du sens.
Il y a d’autres mots qui sonnent comme « analemme ». Il y a les termes mathématiques « lemniscate » (un peu comme un graphique avec une figure en forme de 8), et « lemme » (un théorème mineur utilisé pour prouver quelque chose d’autre, comme ce qu’on fait ici). Il y a aussi « dilemme », qui est ce qui se produit lorsque vous avez deux choses qui essaient d’être vraies en même temps – comme avec le Soleil et le cadran solaire. Il y a même une similarité entre la forme de l’analemme et le symbole pour l’infinité – mais malheureusement, pour celui-ci, il s’agit seulement d’une coïncidence!
Contrôles :
Jour de l’année
Cette commande nous déplace à travers chaque jour de l’année. Vous pouvez utiliser le curseur ou encore les flèches de gauche et de droite de votre clavier pour changer la date. Alors que vous déplacez le curseur, le Soleil va se déplacer à travers les graphiques et tracer l’équation du temps et l’analemme.
Vitesse du jour de l’année
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes. Elle vous permet de déplacer les objets dans les diagrammes à des vitesses variables.
Cliquez et maintenez le curseur enfoncé. Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement.
Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Cette barre de défilement contrôle le jour de l’année. Elle déplace tous les Soleils à travers les jours de l’année, ce qui les amène à tracer les deux graphiques.
Qu’est-ce qui s’en vient maintenant?
Vu que l’analemme nous montre où le Soleil se trouve vraiment dans le ciel pour chaque jour, certaines personnes ont pris ça comme un défi pour photographier le Soleil tous les jours pendant un an, juste pour voir si c’était vraiment le cas! Nous en parlerons plus dans le diagramme 22, où nous allons vous montrer ce à quoi l’analemme ressemble depuis n’importe quel point sur la Terre!
Ce que vous pouvez apprendre :
- Vous pouvez voir comment l’équation du temps se transforme en analemme si on utilise différents moyens de la représenter graphiquement.
- Vous pouvez voir comment le fait de changer la façon dont nous traçons un graphique peut le rendre encore plus utile.
- Vous avez eu une introduction aux graphiques paramétriques.
- Vous pouvez voir l’étrange forme en 8 qu’ils ont placé dans l’océan Pacifique sur tous les globes-terrestres que vous avez pu voir dans votre vie. (Maintenant, vous savez ce que c’est!)
- Vous pouvez voir comment on sait où le Soleil sera dans le ciel pour n’importe quelle heure et n’importe quel jour.
L’analemme dans le ciel
Regardez l’analemme depuis n’importe quel endroit sur la Terre, à n’importe quel moment du jour!
Consultez les instructions du diagramme 22Refermer les instructions
Diagramme 22 :
L’analemme dans le ciel
Ce que vous regardez :
On a utilisé la même sphère que dans les premiers diagrammes. Vous verrez la Terre avec ses pôles, l’horizon et le cercle bleu représentant l’équateur céleste. Vous avez aussi le petit observateur vert, qui peut être placé n’importe où sur la Terre!
Pour l’instant, on a placé l’analemme dans le ciel au lieu de placer le Soleil, la Lune ou les étoiles. Rappelez-vous, l’analemme représente les positions du Soleil à une heure donnée, tous les jours pour une année complète. Vous pouvez déplacer le Soleil le long du contour de l'analemme pour voir où il se trouve dans le ciel à cette heure pour n'importe quel jour donné.
Vous pouvez aussi changer l’heure de la journée. Ceci vous permet de voir la position du Soleil tôt le matin ou tard en soirée. Vous pouvez voir quand le Soleil se lève ou se couche (mais voyez plus bas pour une explication plus détaillée!). Vous pouvez aussi voir à quel point l’analemme change selon différentes latitudes sur la Terre.
Rappelez-vous, l’analemme est une représentation de l’ « équation du temps » - qui nous dit à quel point la position du vrai Soleil dans le ciel est en avance ou en retard par rapport au Soleil « moyen » qui se déplace à la même vitesse tout le temps.
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Montrer l'observateur
Si vous cochez cette case, vous verrez un observateur, un petit bonhomme vert, se tenir sur le dessus de la Terre.
L'horizon qu'on a tracé avec le disque gris et le cercle bleu représentent l'horizon que cet observateur pourrait voir.
Décochez la case pour cacher l'observateur.
Réinitialiser l’horizon
Il n’est pas toujours facile d’obtenir exactement la vue que vous voulez. Utilisez ce bouton pour réinitialiser le diagramme.
Tourner la terre
Vous pouvez tourner la Terre pour placer l'observateur exactement à l'endroit où vous vous trouvez maintenant.
Ceci vous permettra de voir les objets dans le ciel exactement comme ils apparaissent là où vous êtes présentement.
Le nombre qui apparaît à la droite de cette barre de défilement représente la longitude de l'endroit où se trouve l'observateur.
Latitude
Comme dans les premiers diagrammes, ceci vous place à quelque part sur la Terre à une latitude donnée. Vous verrez l’analemme bouger alors que votre position sur la Terre change.
Vitesse du jour de l’année
Une version de la barre de défilement « vitesse » apparaît dans presque tous les diagrammes.
Elle vous permet de déplacer les objets dans les diagrammes à des vitesses variables. Cliquez et maintenez le curseur enfoncé.
Plus vous le faites glisser vers la droite, plus les objets se déplaceront rapidement.
Relâchez-le pour qu’il revienne vers la gauche et arrête le mouvement.
Cette barre de défilement contrôle les mouvements du Soleil le long du contour de l’analemme, pour l’emplacement et le moment de la journée que vous avez établis avec les autres barres de défilement.
Jour de l’année
Changez la date pour déplacer le Soleil le long du contour de l’analemme.
Heure de la journée
Cette barre de défilement vous permet de bouger l’analemme pour voir la position du Soleil à n’importe quelle heure.
NOTE : Cette de barre de défilement montre l’heure solaire locale!
Il est très important de se rappeler que l’heure que vous voyez sur cette barre de défilement n’est généralement pas l’heure que vous voyez sur votre horloge. Elle a été corrigée pour tenir compte de l’équation du temps, bien sûr, puisque l’analemme est basée là-dessus. Mais elle n’est pas corrigée pour des choses comme votre position à l’intérieur de votre fuseau horaire local (longitude), votre altitude, la réfraction atmosphérique ou l’heure avancée d’été. Tout ceci peut amener un décalage allant jusqu’à deux heures par rapport à l’heure affichée sur la barre de défilement!
Il est préférable de considérer que le curseur affiche l’heure « solaire locale », montrant l’heure locale du lever et du coucher du Soleil ainsi que l’heure du midi comme étant des valeurs relatives plutôt que l’heure exacte affichée sur l'horloge. Si vous avez besoin de calculs plus précis pour obtenir l’heure réelle du lever et du coucher du Soleil pour un emplacement précis, plusieurs outils existent en ligne à cet effet.
Nous avons fait en sorte que vous puissiez toujours placer une partie de l’analemme au-dessus de l’horizon, peu importante la latitude sélectionnée. Pour des endroits comme les pôles, vous verrez que l’analemme ne se couche jamais complètement, car il y a des périodes de l’année où le Soleil ne s’y couche jamais. Pour ces endroits-là, vous pouvez choisir n’importe quelle heure – même minuit! Mais pour des latitudes inférieures, quand il y a des moments de la journée où le Soleil ne se rend jamais au-dessus de l’horizon peu importe quel jour nous sommes, nous avons limité la barre de défilement du temps en conséquence. Ça ne fait pas beaucoup de sens de regarder une analemme que vous ne pourriez jamais voir dans le vrai ciel!
Lever et coucher du Soleil
Il y a une caractéristique intéressante de l’analemme que nous devrions vous décrire. Parce que le Soleil doit se placer quelque part le long du contour de l’analemme pour une latitude donnée et une heure de la journée, l’analemme représente vraiment toutes les positions possibles du Soleil pour cette heure précise pour tout le cours d’une année. Ça peut vous aider à trouver la date pour un emplacement donné à laquelle le Soleil se lève ou se couche le plus tôt, ou encore la date où le Soleil se lève ou se couche le plus tard. Pour essayer ceci, réglez en premier la barre de défilement du temps près du lever ou du coucher du Soleil, où une petite partie de l’analemme touche à peine l’horizon. Vous pouvez faire ça à l’ouest ou à l’est, et vous pouvez avoir l’analemme complètement en-dessous de l’horizon, ou complètement au-dessus – il suffit de s’assurer qu’elle touche à peine l’horizon. Une fois que vous l’avez placée comme vous le désirez, vous pouvez alors régler la barre de défilement pour la date jusqu’à ce que le Soleil soit exactement à ce point où l’analemme touche l’horizon.
Disons que vous choisissez le ciel de l’est pour y placer l’analemme, et que vous placez l’analemme pour qu’elle soit au-dessus de l’horizon, en le touchant à peine. Cette disposition vous donnera l’heure du lever du Soleil le plus tardif possible pour cet emplacement. Maintenant, vous pouvez déplacer le curseur pour la date où le Soleil est à ce même point sur l’analemme, en touchant à peine l’horizon. Ce sera la date du lever du Soleil le plus tardif. Ce sera bien sûr à l’heure solaire, mais vous pourrez voir l’emplacement approximatif du lever du Soleil ainsi que la date.
Vous pouvez aussi utiliser l’analemme pour trouver la date du coucher ou du lever du Soleil le plus au Nord ou le plus au Sud pour un emplacement donné. Pour faire ça, il suffit de placer l’analemme pour qu’une partie touche l’horizon le plus au nord ou le plus au sud possible pour cette latitude. Ensuite, déplacez le curseur de la date de nouveau pour placer le Soleil à ce même endroit sur l’horizon, et vous obtiendrez la date que vous recherchiez!
Vous pouvez peut-être penser à d’autres utilisations pour l’analemme : quand est-ce que le Soleil se lèvera ou se couchera à l’est ou à l’ouest pour votre latitude? Pour quel jour(s) va-t-il se lever exactement à 6h00 pour l’équateur? À quelles dates est-ce que le Soleil ne se lève pas à la latitude 78° sud? N’oubliez pas, pour toutes les découvertes que vous faites qui impliquent une heure, cette heure ne sera pas corrigée en fonction des facteurs que nous avons décrits plus haut. Si vous faites l’exercice du « le plus tôt » ou du « le plus tard », ou pour la plupart des événements au nord ou au sud, alors ceux-ci seront beaucoup plus précis.
Photographier l’analemme
Beaucoup de belles photographies (et même des vidéos) de l’analemme sont disponibles en ligne. Elles sont très difficiles à prendre, parce que ça implique d’avoir une caméra installée en permanence pour prendre une photo à la même heure à chaque jour pendant une année complète! La caméra doit être protégée des intempéries, et ne peut pas bouger du tout pendant toute une année. Si vous voulez essayer, choisissez une heure du jour où le Soleil sera au-dessus de l’horizon à tous les jours – et un emplacement où elle ne sera pas bloquée par un arbre ou un édifice à cette heure-là pour n’importe quel jour de l’année. Rappelez-vous qu’il y a plusieurs années, quand les photos ne pouvaient pas être combinées numériquement, les photographes devaient choisir une exposition qui permettait de prendre leurs photos quotidiennes sur le même rouleau de film. Aussi, ils ne pouvaient pas du tout voir le résultat jusqu’à ce que l’année soit terminée! C’était un exploit incroyable, que seul quelques personnes étaient en mesure d’accomplir. Toutefois, ça demeure une expérience intéressante, que vous pourriez tenter d’essayer vous-même!
Ce que vous pouvez apprendre :
- Vous pouvez voir comment l’analemme apparaît pour n’importe quelle latitude sur la Terre, pour n’importe quel moment de la journée où le Soleil est visible.
- Vous pouvez voir comment trouver l’heure du lever ou du coucher du Soleil le plus tôt ou le plus tard pour un emplacement donné.
- Vous pouvez voir comment trouver l’heure du lever ou du coucher du Soleil le plus au nord ou le plus au sud pour un emplacement donné.
- Vous pouvez voir comment l’équation du temps influence la position du Soleil dans le ciel.
- Vous pouvez voir la différence entre votre heure locale et l’heure solaire.
Créez votre propre éclipse lunaire!
Voici un moyen de visualiser ce à quoi une éclipse lunaire ressemble depuis la Terre.
Consultez les instructions du diagramme 23Refermer les instructions
Diagramme 23 :
Créez votre propre éclipse lunaire!
Ce que vous regardez :
On a tout configuré pour que vous puissiez créer une éclipse lunaire! Vous vous tenez debout sur la Terre, en regardant en haut dans le ciel la nuit, et la Lune est à la droite du diagramme par défaut. Alors que le temps avance, elle va se déplacer dans sa trajectoire orbitale autour de la Terre. À cause ça, elle va apparaître en train se déplacer de la droite vers la gauche à travers le diagramme.
La Lune est pleine, ce qui veut dire que le Soleil l’éclaire complètement. Le Soleil est en arrière de vous, donc c’est le jour de l’autre côté de la Terre. Le Soleil qui éclaire la Terre amène l’ombre de la Terre à être projetée dans l’espace, dans votre ciel de nuit. Normalement, vous ne pouvez pas voir cette ombre jusqu’à ce que la Lune s’y retrouve, mais dans ce diagramme, vous serez en mesure de la voir très clairement!
L’ombre terrestre est composée de deux parties : l’ « ombre », qui est la partie centrale sombre de l’ombre terrestre, et une « pénombre », qui est une partie très pâle de l’ombre terrestre qui entoure la partie appelée ombre. Vous pouvez les voir seulement si vous « éteignez » le ciel en utilisant le menu déroulant « ciel ». Le ciel passera ainsi du noir au gris clair, mais l’ombre de la Terre restera en place pour que vous puissiez la voir.
Vous pouvez aussi modifier la distance entre la Terre et la Lune, et entre la Terre et le Soleil. On vous a fourni une commande qui vous permet de modifier ces distances à l’intérieur de la fourchette réelle que nous voyons dans la vraie vie. Chacune de ces distances change légèrement la taille relative de l’ombre, de la pénombre et de la Lune, en se basant sur la géométrie de la situation que vous avez mise en place.
Vous pouvez aussi modifier l’angle de la trajectoire de la Lune, et comment « haute » ou « basse » cette trajectoire sera comparée à l’écliptique. Voici une explication :
L’orbite de la Lune est inclinée d’environ 5,1° degrés par rapport à l’écliptique, et la déclinaison de la Lune peut soit augmenter ou diminuer au nœud de son orbite. On vous a donné un contrôle qui vous permet de déterminer si vous souhaitez que l’éclipse survienne au nœud ascendant ou descendant de la Lune.
Rappelez-vous que d’après le diagramme 9, la Lune doit se trouver près d’un nœud de son orbite pour qu’une éclipse puisse se produire – mais elle n’a pas besoin de se trouver directement à un nœud! Parce que la Lune et le Soleil peuvent être situés à plusieurs degrés avant ou après leurs nœuds réels pendant une éclipse, ça veut dire que la trajectoire réelle de la Lune peut être plus haute ou plus basse qu’une trajectoire directe passant à travers le centre de l’ombre. On vous a donné la possibilité de simuler ceci en bougeant la Lune de haut en bas. N’oubliez pas que ce que vous faites réellement, c’est de déplacer la Lune soit plus tôt, soit plus tard dans son orbite par rapport au nœud.
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Nœud
Utilisez cette commande pour déterminer à quel nœud la Lune se retrouvera, donc si sa déclinaison augmentera ou diminuera.
Ciel
Cette commande vous permet de voir l’ombre de la Terre. Si vous réglez le ciel à « noir », les choses vont ressembler à ce qu’on voit dans la vraie vie, et vous ne pourrez pas voir cette ombre à moins que la Lune se retrouve à l’intérieur. Même si vous réglez le menu déroulant à « gris », alors vous allez pratiquement éteindre le ciel! Vous pourrez voir l’ombre de la Terre être projetée dans l’espace, prête pour que la Lune puisse passer à travers.
L’ombre de la Terre comprend deux parties. Le cercle sombre à l’intérieur est l’ « ombre » elle-même, qui est où toute la lumière du Soleil est bloquée et où une éclipse lunaire serait totale. L’anneau gris pâle autour de l’ombre est la « pénombre », qui est l’endroit où la lumière du Soleil est seulement partiellement bloquée. Si la Lune va dans la région de la pénombre, elle noircit légèrement – mais pas beaucoup.
Vous pourriez lire ou entendre parler du terme « éclipse lunaire pénombrale ». C’est quand la Lune passe seulement à travers la pénombre, passant complètement à côté de l’ombre. Si vous regardiez directement la Lune sans savoir qu’il y a une éclipse pénombrale en cours, vous ne le remarqueriez peut-être même pas!
Hémisphère
Le diagramme montre par défaut les choses telles qu’elles apparaissent dans l’hémisphère nord. Si vous sélectionnez « hémisphère sud » dans le menu déroulant, les choses vont changer pour qu’elles apparaissent comme vous les verriez dans votre propre ciel! La Lune va alors se déplacer de la gauche vers la droite, et va apparaître avec la bonne orientation.
Distance du Soleil
Le Soleil est en arrière de vous dans ce diagramme, et vous ne pouvez pas le voir – mais il fournit l’ombre de la Terre que vous pouvez voir.
Utilisez cette commande pour modifier la distance entre la Terre et le Soleil, ce qui changera légèrement la taille de l’ombre. Le changement de taille est très subtil, mais il est là!
Distance de la Lune
Vous remarquerez un changement marqué de la taille de la Lune lorsque vous ajusterez sa distance. (C’est quelque chose que vous ne pouvez pas remarquer dans la vraie vie à moins d’avoir de l’équipement de mesure astronomique – ou à moins que vous n’ayez entendu dire qu’il allait y avoir une « super lune ». Désolé de vous décevoir, mais ce n’est vraiment rien de plus qu’une Lune plus grande que la moyenne).
Vous remarquerez aussi que la pénombre change de taille. La raison pour ça est qu’on devait garder quelque chose de constant pendant que la distance de la Lune change. Parce qu’il est important de pouvoir voir la taille de la Lune changer, on doit garder la même taille pour l’ombre. Parce que les ombres sont dessinées à la distance de la Lune, cela signifie que la pénombre s’agrandit alors que la Lune s’éloigne. (L’ombre devient en fait plus petite dans la vraie vie alors que la Lune s’éloigne, mais si on avait montré ça, alors vous ne pourriez pas voir la Lune changer de taille.)
Position de la Lune
Souvenez-vous, la Lune doit être à un de ses nœuds pour qu’une éclipse puisse avoir lieu – mais elle n’a pas besoin de se trouver exactement sur le nœud! Elle peut se trouver à quelques degrés de distance de n’importe quel côté du nœud. Ça veut dire que la Lune peut apparaître plus haute ou plus basse que l’écliptique, et cette commande peut vous aider à modéliser ça.
Si vous bougez la Lune de haut en bas en utilisant cette commande, vous la placez en fait plus tôt ou plus tard que le nœud. Ça veut dire que la Lune peut manquer l’ombre complètement (c’est ce qui se passe habituellement). Ou, elle peut passer seulement à travers la pénombre, ou partiellement à travers l’ombre. Ça dépend de où vous la placez!
En utilisant cette commande, vous pouvez configurer quatre types d’éclipse lunaire :
- Éclipse pénombrale partielle :
- La Lune va toucher seulement partiellement la pénombre. Ce type d’éclipse est à peu près impossible à observer, parce que la Lune ne s’assombrit pas beaucoup.
- Éclipse pénombrale :
- La Lune devient complètement recouverte par la pénombre. Vous pourriez remarquer un certain assombrissement, mais encore, ce type d’éclipse est difficile à observer.
- Éclipse partielle :
- La Lune devient partiellement recouverte par l’ombre. C’est très facile à remarquer, parce que la partie de la Lune qui entre dans l’ombre peut devenir très sombre. C’est un énorme contraste par rapport à la partie de la Lune qui se retrouve seulement dans la pénombre.
- Éclipse totale :
- La Lune sera complètement submergée dans l’ombre, et va s’assombrir de beaucoup. C’est une très belle éclipse à regarder!
Les données indiquées à la droite de cette commande vous permettent de savoir de combien de rayons lunaires vous avez déplacé la Lune de haut en bas depuis l’écliptique.
Trajectoire
Cette commande déplace la Lune dans sa trajectoire à travers (ou dépassé) l’ombre. Encore une fois, la commande nous indique de combien de rayons lunaires la Lune s’est retirée du point central de l’ombre, le long de sa trajectoire. Vous pouvez aussi utiliser les flèches de droite et de gauche de votre clavier pour déplacer la Lune, afin d’obtenir un mouvement fluide. Chaque clic sur la flèche de votre clavier représente un peu plus de 30 secondes de mouvement dans la vraie vie. Ça vous montre le rythme lent que prennent toutes les éclipses lunaires!
On doit aussi souligner le fait que la Lune se déplace de la droite vers la gauche alors que vous avancez dans le temps en utilisant la commande pour la trajectoire. C’est parce que la Lune est du côté opposé de la Terre par rapport au Soleil, alors elle se déplace effectivement d’ouest en est dans son orbite (« droite » vers la « gauche »). Pendant une éclipse lunaire, l’ombre de la Terre reste essentiellement immobile dans le ciel, et la Lune se déplace au travers d’elle. C’est vrai – pendant une éclipse lunaire, les mouvements de la Lune que vous voyez ne sont pas dûs à la rotation de la Terre, mais au mouvement de la Lune elle-même dans son orbite autour de la Terre!
À quel point la Lune devient-elle obscure?
Vous remarquerez que quand une partie de la Lune entre dans l’ombre, celle-ci prend une sorte de teinte rougeâtre terne.
Dans la vraie vie, cette coloration peut aller d’un rouge pâle à un rouge très sombre et profond – se rapprochant de « noir pâle ». Dans les cas extrêmes, la Lune peut sembler disparaître complètement – mais c’est rare. Dans ce diagramme, on a choisi de représenter la totalité en utilisant un modèle raisonnablement standard pour montrer à quel point une éclipse lunaire est sombre. Mais rappelez-vous – chacune d’entre elles est légèrement différente!
Les astronomes utilisent une méthode visuelle pour décrire l’obscurité d’une éclipse lunaire totale, essentiellement en la regardant et en la comparant avec les étoiles environnantes, ou en se basant sur leur propre expérience, pour la décrire aux autres. L’échelle qu’ils utilisent est appelée « échelle de Danjon ». Elle utilise des nombres de 0 à 4 (avec 0 qui est le niveau le plus sombre).
Les photos d’éclipses lunaires semblent presque toujours très belles avec du rouge vif ou du orange. C’est parce que le photographe a utilisé une très longue exposition pour rendre la Lune plus brillante qu’elle ne l’est réellement dans le ciel. Cette exposition plus longue permet à des étoiles brillantes d’être aussi photographiées, ce qui crée un beau portrait lunaire.
Pourquoi certaines éclipses sont-elles plus sombres que d’autres? Et pourquoi est-ce que la Lune devient colorée quand elle entre dans l’ombre? Et bien, l’obscurité est liée à la taille de l’ombre, et jusqu’à où la Lune se rend à l’intérieur de l’ombre. Il est assez rare que la Lune passe exactement au centre de l’ombre, alors pendant certaines éclipses, elle ne passe pas à travers la partie la plus sombre et la plus profonde de l’ombre.
Lors d’une éclipse, la Lune semble être de couleur rouille, rouge ou orange. C’est parce que l’atmosphère de la Terre disperse la lumière du Soleil. La lumière du Soleil est bloquée par la Terre, mais l’air autour des contours de la Terre « dévie » une partie de la lumière du Soleil autour. Une partie de cette lumière se rend jusqu’à l’ombre, et selon la quantité de poussière, de fumée, de cendres volcaniques ou de nuages qui sont présents dans ces parties de la Terre, plus ou moins de lumière y sera dispersée dans l’atmosphère.
L’atmosphère de la Terre disperse cette lumière à des endroits qui sont toujours situés à l’endroit où le Soleil (comme vous le verriez depuis ces endroits sur la Terre) est directement sur l’horizon. Parce que la dispersion de la lumière est ce qui amène les levers et les couchers du Soleil à être rouges, les astronomes aiment souligner que la couleur rouge-orange que vous voyez sur la Lune pendant la totalité est l’effet cumulatif de chaque lever et coucher de Soleil sur la Terre se produisant tous en même temps!
Ce que vous pouvez apprendre :
- Vous pouvez voir comment l’ombre de la Terre a deux parties différentes – l’ombre elle-même et la pénombre.
- Vous pouvez voir comment la Lune se déplace à travers l’ombre de la Terre pendant une éclipse lunaire.
- Vous pouvez voir qu’une éclipse lunaire vous donne la chance d’observer la Lune se déplacer dans son orbite.
- Vous pouvez apprendre à propos des différents types d’éclipses lunaires.
- Vous pouvez apprendre pourquoi la Lune prend une couleur rouge ou orange pendant une éclipse totale.
- Vous pouvez apprendre pourquoi les éclipses lunaires surviennent à un rythme très lent – à l’opposé d’une éclipse solaire totale.
Créez votre propre éclipse solaire!
Ce diagramme vous montre la méthode de Bessel pour prédire les éclipses solaires, et vous permet de configurer votre propre éclipse.
Il est fortement recommandé de lire les instructions en premier!
Consultez les instructions du diagramme 24Refermer les instructions
Diagramme 24 :
Créez votre propre éclipse solaire!
Ce que vous regardez :
Voici probablement le diagramme le plus compliqué de tous – et il en a beaucoup à vous montrer!
Quand le diagramme se charge, vous regardez une plaque grise avec un cercle dessus. Le cercle foncé est une Terre « aplatie », et vous pouvez voir l’équateur noir ainsi que les pôles Nord et Sud dessus. Vous pouvez cliquer et faire glisser cette plaque plate pour la faire tourner.
Vous verrez aussi une forme rouge et verte qui ressemble à une ligne – mais en réalité, c’est un cône très long et mince. Si vous zoomez et faites pivoter le diagramme, vous verrez qu’il y a en fait deux cônes, avec leurs pointes réunies et pointant dans des directions opposées. Ce double cône est l’ombre de la Lune, qui est derrière vous à la droite lorsque le diagramme se charge. Cette ombre va se déplacer au-dessus de ce modèle de la Terre plate, et ça va permettre aux gens de voir une éclipse!
Ce plan plat est une coupe transversale de la Terre, dessinée à travers les pôles Nord et Sud ainsi que du centre de la Terre. La Lune est derrière vous. Le Soleil est encore plus loin en arrière de vous que la Lune ne l’est, alors ça amène l’ombre de la Lune à être projetée perpendiculairement sur cette Terre plate. Ça veut dire que l’ombre de la Lune va toujours frapper cette « Terre » à un angle de 90°.
Ça veut dire que peu importe comment les choses sont arrangées, la partie de l’ombre qui croise cette Terre plate sera toujours un cercle parfait – et ça rend tous les calculs beaucoup plus faciles!
(Note : Le cercle n’est pas parfait, parce qu’il y a des montagnes et des vallées sur les bords de la Lune qui créent de petites dentelures dans le contour de son ombre. Mais pour les besoins de ce diagramme, nous assumerons que le cercle est parfaitement rond!)
Ce modèle de « Terre plate » représente exactement le scénario que l’astronome et mathématicien Friedrich Bessel a inventé quand il a créé sa méthode pour prédire les éclipses au début des années 1800. C’est une simplification brillante, car elle nous permet de calculer la taille et la forme de l’ombre, de même que ses mouvements au-dessus de la Terre plate, en utilisant rien de plus que de la géométrie élémentaire et de la trigonométrie.
On a oublié un détail très important à propos du plan fondamental de Bessel. Celui-ci nous a permis de vous montrer quelque chose qui sera très utile à notre discussion. Le plan fondamental de Bessel se déplace dans l’espace pour que les pôles nord et sud soient toujours alignés avec ceux de la Terre. C’est absolument nécessaire si on veut pouvoir effectuer les calculs détaillés d’éclipses que le modèle nous permet. Dans notre plan, on permet à la Terre de se déplacer comme elle le fait lorsqu’elle se déplace dans son orbite – sauf qu’on garde le plan fixe dans une position où ses pôles sont alignés avec ceux de la Terre seulement pendant les solstices d’été et d’hiver. Ça nous permettra de vous montrer TRÈS clairement qu’en provoquant des éclipses solaires, la Lune ne se déplace jamais d’aucune autre manière que dans son orbite habituelle – qui est inclinée de 5,1° vers le haut ou vers le bas par rapport à l’écliptique.
L’ombre de la Lune
Il y a deux parties dans l’ombre de la Lune – la partie rouge et la partie verte. Nous aurons besoin d’un autre diagramme pour vous expliquer pourquoi c’est comme ça, mais nous utiliserons un dessin classique que vous voyez tout le temps quand on explique une éclipse. Gardez à l’esprit que ce dessin n’est pas à l’échelle; le cône qu’on montre ci-dessous est réellement très long et mince – comme dans le diagramme principal!
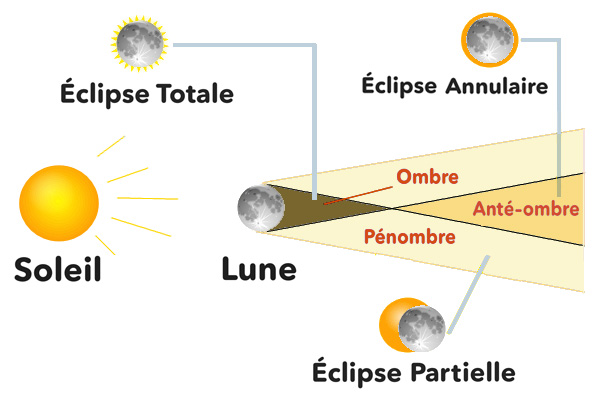
(www.wpclipart.com)
Vous remarquerez que l’ombre de la Lune a été dessinée comme étant un triangle. En réalité, dans l’espace tridimensionnel, ce triangle sera en fait un cône. Depuis la Lune jusqu’au bout de ce cône, il s’agit de la véritable « ombre » de la Lune. Si vous êtes à l’intérieur de la région de cette ombre, le Soleil sera complètement bloqué. Tout est très bien indiqué dans l’image ci-haut, mais on a colorié cette partie du cône de l’ombre en vert dans notre diagramme.
Si vous prolongez ces lignes qui forment les côtés du cône gris, vous verrez qu’elles forment un autre cône inversé qui continue à travers l’espace. Il s’agit de l’ « anté-ombre », et si vous êtres à l’intérieur de cette région du cône, alors la Lune va sembler recouvrir le Soleil, mais elle ne sera pas assez large pour le recouvrir complètement. Ça veut dire que vous verrez un anneau de Soleil autour des contours de la Lune – une éclipse « annulaire ». On a colorié cette partie du cône de l’ombre en rouge dans notre diagramme.
(Veuillez noter qu’ « annulaire » ne veut pas dire « annuel »! Les deux mots sont très différents. « Annulaire » vient d’un mot latin qui veut dire « anneau ». « Annuel » veut dire quelque chose qui survient à chaque année, ce qui n’est pas le cas ici.)
Disons que vous vous trouvez sur la Terre plate, et que cette ombre passe au-dessus de vous. Si vous étiez dans la partie verte du cône, vous verriez une éclipse solaire totale. Si vous étiez dans la partie rouge, vous verriez une éclipse annulaire. Jusqu’ici, tout va bien.
Mais quand le diagramme se charge, il semble que peu importe où vous vous trouvez, vous allez toujours vous retrouver dans la partie verte du cône! Comment la partie rouge peut-elle éventuellement toucher la Terre plate? Patience… Nous y arriverons!
Une fois que vous commencez à utiliser les contrôles, vous verrez que vous pouvez placer ce cône où vous voulez – en haut, en bas, à droite ou à gauche. Vous serez aussi capable de le déplacer au-dessus de la Terre plate, comme la Lune se déplace son orbite et que l’éclipse a lieu. Mais vous serez aussi capable de modifier les distances entre la Terre et la Lune, et entre la Terre et le Soleil! Si vous faites ça, alors vous verrez la forme du cône de l’ombre changer, et il y aura des configurations que vous pourrez mettre en place qui vous permettront de faire toucher la partie rouge du cône à la Terre plate.
Vous pourriez vouloir « zoomer » dans le diagramme, pour pouvoir voir le contour rond de l’ombre de la Lune sur la Terre plate. Vous verrez qu’il s’agit d’un cercle – mais pas d’un très gros!
La pénombre
On a aussi une case à cocher appelée « Montrer la pénombre ». Si vous cochez cette case, vous verrez la partie externe de l’ombre de la Lune, où le Soleil est seulement partiellement bloqué. Elle ressemble à un cylindre, mais il s’agit en fait de la partie finale d’un très long cône en pente douce. Si vous êtes sur la Terre plate, et que cette partie appelée pénombre de l’ombre passe au-dessus de vous, alors vous verrez une éclipse solaire partielle – peu importe que ce soit la partie rouge ou verte qui soit en jeu pour les distances que vous avez établies!
Mais la Terre n’est pas vraiment plate!
Cette Terre plate peut être très utile pour visualiser tout cela, mais on sait que la Terre n’est pas vraiment plate. On l’a juste imaginée comme ça pour simplifier l’image – et les mathématiques! Mais quand vous changez le mode dans le menu déroulant qu’on vous a fourni, alors les choses commencent à devenir intéressantes.
Si vous utilisez le mode « 3D », alors la Terre place va se transformer en une Terre ronde – mais l’ombre de la Lune sera toujours directement où elle était. Maintenant, si vous « zoomez », vous verrez que dépendamment de où l’ombre est située, l’intersection de la Terre ronde et de l’ombre en forme de cône est vraiment compliquée. C’est une sorte d’ovale, mais il peut être plus circulaire si l’ombre est près du « milieu » de la Terre. Ça peut prendre une forme très bizarre si l’ombre est près du bord de la Terre. Mais la chose la plus importante à se rappeler est que c’est toujours a même ombre qu’on a vue avant! L’ombre ne change pas de forme, mais quand on la projette depuis le plan de la « Terre plate » vers la vraie « Terre ronde », la forme de l'intersection devient alors pas du tout circulaire. Les maths qu’on aurait à utiliser pour décrire ça seraient très compliquées, et c’est pourquoi il est beaucoup plus facile de débuter en imaginant ce contour parfait du cercle sur la Terre plate.
En passant, il est toujours vrai que n’importe qui se retrouvant situé à l’intérieur de la partie verte de l’ombre de la Lune verra une éclipse totale, et n’importe qui dans la partie rouge de l’éclipse va voir une éclipse annulaire. C’est juste que pour maintenant, on a une idée de exactement où sur la Terre ils doivent se tenir debout pour voir l’éclipse.
Si vous avez activé la pénombre, vous verrez aussi ses contours sur la surface de la Terre. N'importe qui à l'intérieur de cette très grande région, mais à l'extérieur du cône rouge ou vert, verra une éclipse partielle. Encore (et il est vraiment important de s’en rappeler), tout le monde dans cette région périphérique pénombrale de l’ombre va voir une éclipse partielle, peu importe si les gens à l’intérieur de l’ombre rouge ou verte voient une éclipse totale ou annulaire. En fait, si nous n’avez pas dit aux gens dans la pénombre quel genre d’éclipse était en cours dans le centre de cette ombre, ils n’auraient aucun moyen de le savoir.
Dans le menu déroulant « Mode », vous verrez aussi «3D + masquer ». Ce réglage vous permet de cacher la partie des ombres qui est du côté arrière de la Terre plate. Il y a des situations qui pourraient survenir où il est plus facile de voir ce qui se passe si vous avez ce réglage mis en place.
Vous avez aussi des contrôles pour déplacer le diagramme de haut en bas ou de gauche à droite. C’est pratique si vous devez « zoomer » de beaucoup à l’intérieur et que la partie de la Terre que vous voulez voir est sortie du cadre du diagramme.
Finalement, vous avez des contrôles pour vous permettre de spécifier si l’éclipse survient au nœud ascendant ou descendant de la Lune, et pour incliner la Terre correctement selon le jour de l’année. L’inclinaison est importante, parce que selon la partie de l’année dans laquelle on est, la Terre peut être inclinée dans n’importe quel direction par rapport à la trajectoire de la Lune.
Distances de la Lune et du Soleil
Tout comme dans le diagramme précédent, vous pouvez modifier les distances entre la Terre et la Lune ainsi qu’avec le Soleil, et vous verrez les formes des ombres changer. Vous remarquerez que la distance du Soleil a un effet sur les longueurs relatives des parties rouge et verte de l’ombre, mais la distance de la Lune est ce qui a le plus grand impact sur ces longueurs jusqu’à maintenant.
Types d’éclipses
Sur la Terre plate, les choses sont simples. En se basant sur les distances que vous avez établies pour le Soleil et la Lune, la partie rouge ou la parte verte de l’ombre de la Lune vont créer une éclipse sur la « Terre ». Si elle est rouge, alors une éclipse annulaire sera visible dans cette partie de l’ombre. Si elle est verte, alors l’éclipse sera totale.
Par contre, lorsque vous passez à une Terre ronde – les choses deviennent compliquées. La plupart du temps, le type d’éclipse qu’on aura sur la Terre plate sera le même que l’éclipse qu’on aura sur une Terre ronde. Mais ce n’est pas nécessairement toujours le cas!
Si vous configurez une éclipse annulaire sur la Terre plate, puis que vous allez à une Terre 3D, vous verrez que l’éclipse sur la Terre ronde sera toujours annulaire. De même, si vous configurez une éclipse totale sur la Terre plate, habituellement, l’éclipse sur la Terre 3D sera aussi totale.
Mais il est aussi possible de tout régler pour que le bout du cône de l’ombre ne soit pas très haut au-dessus de la Terre plate. Dans ce cas, il peut arriver que l’éclipse sur la Terre 3D soit annulaire au début et à la fin de la trajectoire, mais qu’elle devienne totale au milieu! Ce type d’éclipse est appelée « annulaire-totale », et parce que des circonstances spéciales sont requises, ces éclipses sont raisonnablement rares. Vous pouvez en configurer une en réglant la distance de la Lune et du Soleil pour que le bout du cône de l’ombre soit juste au-dessus de la Terre plate – comme on l’a décrit.
On indique le type d’éclipse au-dessus des nombres indiquant la distance du Soleil. Ça vous indique quel type d’éclipse a été configuré. Normalement, vous verriez que l’éclipse est soit « annulaire » ou « totale ». Mais si vous avez configuré cette situation comme on l’a décrite plus haut, alors l’éclipse sera affichée comme étant « annulaire-totale ». Ça veut dire qu’elle débutera comme étant annulaire, elle changera pour une totale, et reviendra à annulaire encore.
À noter que pour une éclipse annulaire-totale, il est possible d'arranger les choses dans la vraie vie pour que la portion annulaire de l'éclipse soit élimintée à un bout ou l'autre de sa trajectoire. Ce n'est pas possible dans notre diagramme, et on va vous donner plus de détails à propos de ça ci-bas.
Contrôles :
Vous pouvez écarter ou rapprocher les doigts ensemble (pincer) sur un écran tactile ou encore utiliser la fonction « zoom » à gauche de l’écran pour agrandir ou réduire le diagramme. Vous pouvez aussi utiliser les boutons de gauche et de droite de la souris pour déplacer et faire pivoter l’ensemble du diagramme.
Sélectionner éclipse prédéfinie
À la demande générale, nous avons pré-programmer des éclipses réelles dans ce simulateur, pour vous montrer à quel point cette géométrie peut être exacte. Dans le coin supérieur gauche, vous verrez un bouton qui dit « Sélectionner éclipse prédéfinie ». Si vous cliquez sur ce bouton, vous verrez une liste d’éclipses à la droite. Déplacez le curseur de votre souris au-dessus d’une date pour voir les informations à propos de cette éclipse. Cliquez sur la date pour charger les données sauvegardées dans la simulation. Ensuite, vous pouvez voir les choses pareil comme si vous aviez créé l’éclipse vous-même! Rien n’a été ajouté à la simulation – on a juste chargé les valeurs dans les contrôles pour vous permettre de voir une véritable éclipse passée ou future!
On doit vous prévenir que ce diagramme est un outil éducatif, et non PAS un outil rigoureux de prédiction des éclipses. Les trajectoires affichées que vous verrez pour ces éclipses présélectionnées sont très près des véritables trajectoires (en fait, elles sont surprenamment précises!), mais elles ne sont pas parfaites. Elles ne peuvent pas être parfaites car on n’a pas intégré tous les facteurs de correction dans les maths qui seraient utilisées si nous ferions des calculs rigoureux. On va vous expliquer certains des détails plus bas, mais s’il-vous-plaît rappelez-vous que, surtout au début et à la fin de la trajectoire, l’ombre pourrait être un peu décalée.
Réinitialiser l’écliptique
Ce contrôle va remettre à niveau l’écliptique. Il s’agit de la ligne rouge qui traverse la Terre, qui montre la trajectoire du Soleil pendant le cours d’une année.
Réinitialiser l’équateur
Ce contrôle va remettre à niveau l’équateur. Il s’agit de la ligne bleue qui traverse la milieu de la Terre.
Lumière du jour
Ce bouton place le Soleil directement en arrière de vous, pour que vous puissiez regarder la partie de la surface de la Terre qui se retrouve complètement dans la lumière du jour. Ça peut vous aider à vous orienter dans le cas où vous voudriez voir ce qui se passe pendant le milieu de l’éclipse.
Lorsque vous appuyez sur ce bouton, vous pourriez penser que l’ombre de la Lune a soudainement disparu. Parce que vous vous êtes alignés parfaitement avec le Soleil et la Lune, vous trouverez (si vous « zoomez ») que vous regardez directement en plein milieu de l’ombre! Cela donne l’impression qu’il s’agit d’un cercle, tout comme c’était le cas sur la Terre plate. Il suffit de pivoter le diagramme en peu en le faisant glisser avec votre souris, et vous verrez de nouveau les côtés de l’ombre!
Nœud
Ce contrôle détermine si la Lune va bouger « vers le haut » ou « vers le bas » à son angle standard de 5,1° par rapport à l’écliptique.
Mode
Ce contrôle vous permet de montrer l’éclipse qui se produit soit sur une Terre plate ou sur une Terre ronde. Le mode « 3D + Masquer » vous permet de cacher la partie de l’ombre de la Lune qui est du côté arrière de la Terre plate. C’est extrêmement pratique pour montrer où la trajectoire de l’éclipse débute ou se termine à cause du lever ou du coucher du Soleil local.
Montrer pénombre
Parfois, vous voulez seulement voir l’ombre ou l’anté-ombre – la partie de l’ombre de la Lune qui est l’acteur principal dans le grand jeu de l’éclipse. Dans ce cas, désactivez la pénombre en utilisant cette case à cocher. Si vous voulez montrer où l’éclipse solaire est partielle, alors vous pouvez l’activer.
Rotation de la Terre
Cette case à cocher est active seulement si le « Mode » sélectionné est celui de la Terre ronde. Si vous l’activez, alors la Terre va tourner à la bonne vitesse lorsque vous utilisez le contrôle de la « Trajectoire » pour déplacer l’ombre de la Lune. Si vous la désactivez, vous verrez seulement l’ombre de la Lune bouger. Ça peut vous aider à visualiser les changements dans l’éclipse sans être distrait par la rotation de la Terre en arrière-plan.
Masquer les contrôles
Après avoir zoomé très loin, certains contrôles peuvent bloquer la vue. Cette case à cocher réduit le nombre de contrôles au strict minimum, vous permettant de zoomer et de déplacer la vue autour, sans avoir autant de barres de défilement dans le chemin. Décochez la case pour ramener les contrôles – ce qui vous permettra de modifier les réglages et de créer votre propre éclipse!
Distance du Soleil
Le Soleil éclaire la Lune, qui ensuite projette son ombre sur la Terre. La forme de cette ombre varie, selon l’emplacement exact du Soleil et de la Lune. Parce que l’ombre détermine la durée et le type de l’éclipse, ces distances sont importantes!
Ce contrôle vous permet de établir la distance entre le Soleil et la Terre, changeant la forme de l’ombre de la Lune au passage.
Distance de la Lune
La distance de la Lune a un gros impact sur la taille et la forme de son ombre. Si vous prenez une vue de côté du diagramme, et changez la distance de la Lune d’un extrême à l’autre, vous verrez à quel point ça fait une grande différence pour l’ombre!
Jouez avec ces deux distances pour avoir une idée de l’impact qu’elles ont eu sur la forme de l’ombre – et le type d’éclipse que les gens sur la Terre pourront voir. Vous pourrez clairement le peu de marge qui existe entre les paramètres requis pour une éclipse totale vs une éclipse annulaire.
Position de la Lune
Ce contrôle déplace la Lune « vers le haut » ou « vers le bas » par rapport à l’écliptique. Rappelez-vous, dans le diagramme 23, les éclipses ne surviennent pas nécessairement quand la Lune est exactement à un nœud – elle peut être à plusieurs degrés d’un côté ou de l’autre du nœud. Ce contrôle simule la situation en déplaçant la Lune plus loin de l’écliptique, ce qui amène la Lune à bouger dans une trajectoire qui est aussi loin que vous le désirez du centre de la Terre.
La donnée à la droite de la barre de défilement indiquent à quelle distance vous avez déplacé l'ombre de la Lune, exprimée avec des unités de mesure représentant le rayon de la Terre.
Jour de l’année
La Terre a une inclinaison fixe de 23,4° par rapport à l’écliptique. Mais parce que la Terre pointe toujours dans la même direction du ciel, cette inclinaison se présente au Soleil comme changeant au cours de l’année. C’est la même chose qui amène le Soleil à changer de déclinaison d’un mois à l’autre. Parce que les éclipses peuvent survenir à n’importe quel moment de l’année, le Soleil pourrait voir la Terre comme étant inclinée d’un côté, ou de l’autre côté, ou pas du tout, pendant l’éclipse. Ce contrôle vous permet de modéliser cela..
Déplacez le contrôle complètement à la droite ou à la gauche pour obtenir une éclipse survenant en juin. Placez le contrôle dans le milieu pour simuler une éclipse survenant en janvier. Ou placez-le n’importe où entre les deux!
Tournez la Terre
Vous pouvez tourner la Terre de n’importe quel bord que vous voulez, pour simuler une éclipse survenant n’importe où sur la Terre. Si vous avez activé « Rotation de la Terre », alors la Terre tournera à partir de ce point alors que vous déplacez l’ombre de la Lune.
Mouvement panoramique
Si vous avez « zoomé » beaucoup à l’intérieur, il pourrait y avoir des choses sur le bord de la Terre qui se passent en-dehors de votre écran. Utilisez ce contrôle pour ajuster les choses pour que vous puissiez les voir. Ces contrôles ne réinitialise pas les mouvements de la Lune ou de la Terre – ça change uniquement votre vision des choses.
Trajectoire
Ce contrôle vous permet de déplacer l’ombre de la Lune de la gauche vers les droite, à travers la face de la Terre ronde ou plate. (En supposant que vous regardez le côté de la Terre où c’est le jour.)
La Lune se déplace de la gauche vers la droite dans le diagramme, parce qu’elle est entre la Terre et le Soleil (et rappelez-vous, il est derrière vous!). La Lune se déplace toujours dans son orbite de l’ouest vers l’est dans le ciel, alors ça veut dire de la gauche vers la droite quand elle est à ce point dans son orbite.
(D’ouest en est? La Lune ne se lève-t-elle pas à l’est et ne se couche-t-elle pas à l’ouest? En effet, oui – mais ce mouvement apparent est causé par la rotation de la Terre, et non pas par le mouvement orbital réel de la Lune elle-même. Si la Terre ne tournait pas, vous pouvez être certain que vous verriez la Lune se déplacer d’ouest en est à travers le ciel – et elle prendrait environ deux semaines entre son lever et son coucher! Nous l'avons vu dans le diagramme 10a.)
Si vous êtes en mode 3D, avec « rotation de la Terre » activée, vous verrez la Terre tourner à la bonne vitesse, en se basant sur la distance de la Lune que vous avez établie. Vous verrez très clairement que la Lune se déplace dans son orbite plus rapidement que la vitesse à laquelle la Terre tourne, parce que l’ombre traverse la Terre plus vite que les continents ne se déplacent. Ça fait du sens, puisque la Lune doit recouvrir l’entièreté de la circonférence de son orbite en un mois, pendant que la Terre doit seulement recouvrir la circonférence de sa surface en un jour. (Voir plus bas pour plus de calculs détaillés.)
Aussi, dans ce diagramme, les données inscrites à la droite de la barre de défilement pour la trajectoire indiquent à quelle distance l’ombre de la Lune est (le long de la trajectoire de ses mouvements) depuis le centre de la Terre, exprimée en rayons de la Terre.
Vous pouvez utiliser les flèches de gauche et de droite de votre clavier, à n’importe quel moment pour déplacer l’ombre le long de sa trajectoire. Quand vous faites ça, vous pouvez estimer que tout se déplace au rythme d’environ 1 minute pour chaque frappe de touche du clavier.
Pourquoi l’éclipse se déplace d’ouest en est?
On a exploré ce concept en détails dans le diagramme 10a, mais voici un résumé :
La Lune se lève à l’est et se couche à l’ouest à cause de la rotation de la Terre. L’éclipse se déplace d’ouest en est à cause du mouvement de la Lune dans son orbite. Parce que la Lune se déplace dans son orbite dans la même direction que la Terre tourne, il est important de savoir laquelle tourne plus vite. Si la Terre tournait plus vite que la Lune, alors l’ombre se déplacerait en effet d’est en ouest à travers la Terre – mais ce n’est pas le cas.
[Note: Ça peut arriver, pour de très rares éclipses polaires où l’ombre passe « au-dessus » d’un pôle et touche la Terre du côté antisolaire du pôle. C’est un cas très rare et inhabituel, mais vous pouvez le modéliser dans ce diagramme si vous voulez!]
Voici les calculs approximatifs pour montrer que la Lune se déplace plus vite dans son orbite que la Terre prend pour effectuer une rotation. La distance moyenne entre la Lune et la Terre est de 384 400 km. Le rayon de la Terre est d’environ 6 370 km. Maintenant, nous pouvons calculer :
- La Lune doit parcourir la circonférence complète de son orbite, qui est 2 × pi × 384 400 ≈ 2,4 million km, en 28 jours. C’est environ 86 000 km par jour.
- La surface de la Terre doit parcourir sa propre circonférence, qui est 2 × pi × 6 370 ≈ 40 000 km, en un jour.
Ça veut dire que la Lune se déplace en moyenne à un peu plus du double de la vitesse que la Terre prend pour effectuer sa rotation! C’est pourquoi, dans la très grande majorité des cas, les éclipses progressent toujours d’ouest en est au-dessus de la Terre.
Quelque chose de plus
Ce diagramme est très sophistiqué dans ce qu’il peut vous montrer. En sélectionnant le jour de l’année, puis en déterminant la position de la Lune et la rotation de la Terre en faisant suffisamment attention, vous pouvez modéliser presque toutes les éclipses que vous souhaitez. Mais encore une fois, ce diagramme est un outil éducationnel – pas un calculateur d’éclipses! On a omis quelques détails très mineurs qui nécessiteraient d’être pris en considération pour pouvoir prédire les éclipses avec une grande précision. Si vous voulez poursuivre plus loin votre étude des éclipses, le matériel de référence est disponible en ligne!
Quels détails avons-nous omis? Et bien, la distance entre la Lune et la Terre change en fait pendant les trois heures pendant lesquelles l’éclipse prend place. Ça change légèrement la forme de l’ombre. Dans le diagramme, on vous a laissé régler la distance du Soleil et de la Lune, mais alors elles demeurent constantes pendant l’éclipse. Vous ne remarqueriez pas la différence à l’échelle de ce diagramme, mais nous devrions prendre ce changement de la distance lunaire en compte pour produire des prédictions d’éclipses qui seraient précises à la seconde près.
Aussi, nous n’avons pas tenu compte que la Terre plate, qui est toujours perpendiculaire à l’ombre de de l’axe de la Lune, tourne très légèrement pendant l’éclipse à cause des mouvements de la Lune dans son orbite. Ça peut introduire de légers changements dans l’ombre dans certains cas très spéciaux qui vont au-delà de l’objectif de ce diagramme. C’est aussi la raison pour laquelle ce diagramme ne peut pas modéliser une éclipse annulaire-totale lors de laquelle l’éclipse débute ou se termine en éclipse totale.
De plus, on a utilisé les valeurs « génériques » de l’inclinaison réelle de la Terre par rapport au Soleil pour les dates du calendrier. En réalité, celles-ci diffèrent légèrement d’une année à l’autre. D’utiliser les valeurs exactes dépasserait la portée de ce diagramme, nous nous contentons donc d’une approximation très proche.
Finalement, la Terre n’est pas une sphère parfaite comme on vous l’a montré dans le diagramme. La Terre est légèrement bombée pour former ce qu’on appelle un « sphéroïde oblat ». Vous ne remarqueriez jamais la différence entre ça et une sphère parfaite avec l’échelle de notre dessin, mais dans la vraie vie, cet « aplatissement » léger de la Terre est quelque chose qu’on doit prendre en considération si on veut dessiner avec précision la forme de l’ombre de la Lune sur sa surface.
Quand même, les trajectoires sont remarquablement précises, considérant à quel point nous avons simplifié les maths!
Ce que vous pouvez apprendre :
- Vous pouvez voir comment l’ombre de la Lune a trois parties différentes – l’ombre, la pénombre et l’anté-ombre.
- Vous pouvez apprendre la différence entre une éclipse annulaire et une éclipse totale.
- Vous pouvez voir comment la distance changeante entre la Terre et la Lune a un grand impact sur le type d’éclipse qu’on peut voir depuis la Terre.
- Vous pouvez voir les bases de comment la méthode de Bessel aide à prédire les éclipses.
- Vous pouvez visualiser l’ombre de la Lune qui se déplace à travers la Terre de plusieurs façons différentes.
- Vous pouvez voir à quoi ressemble le contour de l’ombre d’une éclipse au milieu et aux extrémités de la trajectoire.
- Vous pouvez apprendre pourquoi l’ombre de l’éclipse se déplace (presque) toujours à travers la Terre d’ouest en est.
- Vous pouvez voir à quel point il y a une grande proportion de la surface de la Terre qui peut voir une éclipŝe partielle, alors que seulement une très petite proportion peut voir la totalité.
- Vous pouvez apprendre pourquoi les trajectoires de l’éclipse peuvent prendre plusieurs formes différentes pour différentes éclipses.
Orbites
Apprenez à propos de la vitesse orbitale, de la hauteur et des orbites géosynchrones des satellites.
Consultez les instructions du diagramme 25Refermer les instructions
Diagramme 25 :
Orbits
Il est impossible de parler très longtemps de l’espace sans prendre en considération les orbites. Il y a tellement d’objets dans l’espace qui orbitent autour d’un corps plus grand qu’il est difficile de faire une liste de toutes les différentes possibilités :
- La Terre et les autres planètes orbitent autour du Soleil.
- La Lune orbite autour de la Terre.
- Les satellites qui contrôlent la télévision par satellite, les téléphones et l’Internet orbitent autour de la Terre.
- Le télescope spatial Hubble et la Station spatiale internationale orbitent autour de la Terre.
- Les vaisseaux spatiaux sont mis en orbite autour des corps sur lesquels ils se préparent à atterrir.
- Des étoiles doubles et multiples orbitent les unes autour des autres.
- Toutes les étoiles dans la galaxie orbitent autour du centre de la galaxie.
Dans la plupart de ces cas, on a un très petit objet qui voyage à travers l’espace dans une orbite autour d’un corps beaucoup plus grand. C’est le cas qu’on va prendre en considération dans ce diagramme.
Qu’est-ce qu’une orbite?
Tout ce qui est près d’un très grand corps (comme la Terre) ressent les effets de la gravité du grand corps. Toutes les choses qu’on voit autour de nous sont attirées vers la Terre par sa gravité, et on peut voir cet effet quand un objet « tombe » vers la Terre. L’objet va continuer de tomber jusqu’à ce qu’il soit arrêté soudainement en frappant la surface de la Terre – sinon, il se rendrait jusqu’au centre de la Terre.
Mais si vous lancez quelque chose horizontalement, l’objet va voyager à une certaine distance horizontalement avant de tomber et de frapper le sol. Plus vous lancez fort, plus loin de vous l’objet ira jusqu’à ce qu’il frappe finalement la Terre.
Mais si vous lancez l’objet suffisamment fort, il voyagerait si loin horizontalement qu’au moment où cet objet est supposé tomber à l’endroit où la Terre devrait se trouver, la courbe de la Terre ferait en sorte qu’il n’y aurait pas de sol où tomber! Votre objet continuerait à se déplacer horizontalement, la Terre continuerait de s’ éloigner et l’objet ne frapperait jamais le sol. Il serait en « orbite » autour de la Terre.
C’est ce que sont les orbites : un objet se déplaçant si rapidement (dans une direction parallèle à la surface de la Terre) qu'en tombant, la Terre continue de s'éloigner de cet objet pour qu'il ne puisse jamais toucher le sol.
Il est logique que si un objet est proche du sol, il doit se déplacer VRAIMENT vite pour que cela se produise. Il est plus facile de maintenir une orbite alors qu’on va plus haut dans le ciel, parce qu’il y a plus de place pour que l’objet puisse « tomber » avant qu’il ne rencontre la Terre. Il y a aussi moins de friction atmosphérique dans l’espace, alors on n’a pas à se soucier du vent qui pourrait ralentir notre objet et causer un « déclin » de son orbite.
On peut calculer la vitesse à laquelle on devrait lancer un objet pour obtenir une orbite en se basant sur sa hauteur. Toutefois, on doit aussi tenir compte de la masse de la Terre pour établir une formule de calcul. Si la Terre aurait une plus grande masse, alors elle aura une plus forte gravité. Les objets tomberaient vers elle plus rapidement* et ils devraient se déplacer plus vite pour maintenir leur orbite.
*Techniquement, l’« accélération » de l’objet serait plus grande, mais on tente de rester le plus possible en-dehors des cours de physique!
Le rayon de la Terre est important seulement parce qu’on veut parler de la hauteur de notre objet au-dessus de la surface de la Terre. Ça ne fait pas beaucoup de sens de parler de la hauteur au-dessus du centre de la Terre, vu qu’on ne vit pas au centre de la Terre!
Qu’est-ce qui n’a en fait aucune importance dans tout ceci? La masse du satellite lui-même. C’est exact – à moins que le satellite soit suffisamment massif qu’il pourrait être comparé à la Terre, sa masse ne fait tout simplement pas de différence dans les formules! Ça va arriver lorsque vous avez un objet conçu par l’homme qui orbite autour d’une planète ou de la Lune. Ce ne sera PAS le cas pour des situations comme la Terre avec la Lune, une étoile double, un large vaisseau spatial avec un minuscule astéroïde, ou même la Terre avec le Soleil. Dans ces cas, les deux objets ont un effet gravitationnel non-négligeable entre eux, et les maths deviennent beaucoup plus compliquées! Ces cas ne sont pas représentés dans notre diagramme.
On a aussi simplifié grandement les choses en rendant nos orbites circulaires. Dans la vraie vie, ce ne sera jamais le cas, parce qu’une orbite parfaitement circulaire est impossible à atteindre. On peut s’en rapprocher, donc les maths représentent une très bonne approximation – mais comme on l’a vu dans le diagramme sur les lois de Kepler, les vraies orbites seront toujours elliptiques.
On devrait aussi mentionner que, alors qu’on a dessiné la Terre comme étant le corps principal dans ce diagramme, on aurait pu placer n’importe quelle planète, Lune ou étoile à sa place. Vous êtes en mesure d’ajuster différents réglages pour la Terre dans le diagramme avec une vaste gammes de tailles et de masses, et ça vous permet de simuler ce qui se passerait si votre objet principal était beaucoup plus grand ou petit que la Terre.
Ce que vous regardez :
La Terre est au centre du diagramme, et on a tracé un cercle autour qui représente l’orbite d’un corps plus petit – comme un satellite. Vous pouvez ajuster quatre choses dans ce diagramme :
- Le rayon de la Terre
- La masse de la Terre
- La hauteur de l’orbite du satellite
- La période rotationnelle de la Terre
Quand vous configurez les trois premières choses, vous verrez que la vitesse orbitale et la période du satellite changent. C’est parce que ces trois choses sont tout ce que vous devez savoir pour être en mesure de trouver à quelle vitesse le satellite doit se déplacer horizontalement pour pouvoir demeurer en orbite. Cette vitesse mène après à la période orbitale – combien de temps ça prend pour faire le tour de la Terre une fois.
Vous pourriez croire qu’on a besoin de plus de données, mais ce n’est pas le cas. Comme on l’a mentionné plus tôt, nous n’avons pas besoin de la masse du satellite.
Si vous pensez qu’on a oublié de parler de la période rotationnelle de la Terre, ce n’est pas le cas, ça s’en vient!
Contrôles :
Masse de la planète
Vous pouvez ajuster la masse de la Terre en la rendant très petite ou très grande. Pour vous aider, on a placé des marques aux endroits où le Soleil, la Terre,
la Lune et un petit astéroïde devraient se trouver. Le bouton « Réinitialiser » permet de remettre le curseur à la bonne valeur pour la masse de la Terre.
Rayon de la planète
Vous pouvez ajuster la taille de la Terre. Encore une fois, on a placé des marques sur la barre de défilement pour montrer le Soleil, la Terre,
la Lune et un petit astéroïde. Aussi, le bouton « réinitialiser » ramène votre rayon à celui de la Terre.
Hauteur de l’orbite
Il s’agit de la hauteur de votre satellite au-dessus de la surface de la Terre. Alors que vous augmentez la hauteur, vous verrez que la vitesse orbitale ralentit, et que la période devient plus longue.
Calculer l’orbite géostationnaire
Cette commande requiert certaines explications :
Plusieurs immeubles utilisent une antenne satellite pour recevoir les signaux de la télévision. Ces antennes peuvent êtres petites ou grandes, mais elles sont toujours installées sur le toit ou le côté de la maison, ou sur un poteau au sol. Une fois qu’elles sont installées et configurées, elles ne bougent jamais. Elles sont pointées en direction d’un satellite qui envoie le signal, et c’est comme ça que le téléviseur reçoit les données qu’il affiche à l’écran.
Mais comment est-il possible qu’une antenne qui ne bouge jamais puisse rester pointée en direction du satellite qui orbite autour de la Terre? Le satellite ne se déplace-t-il pas dans l’espace? Il ne se tient certainement pas immobile là-haut dans les airs!
Il est possible de placer un satellite à la bonne hauteur dans le ciel pour que sa période orbitale corresponde exactement à la vitesse à laquelle la Terre effectue sa rotation. Le satellite se déplace certainement dans son orbite, mais la Terre se déplace aussi! Si la vitesse de la Terre et du satellite sont exactement les mêmes, alors il nous semblerait que le satellite est parfaitement immobile dans le ciel. C’est très pratique, parce qu’on peut alors pointer nos antennes satellites et on sait qu’on sera toujours en mesure de recevoir les signaux pour la télévision provenant du satellite.
Si ce satellite effectuerait son orbite à une altitude plus haute ou plus basse au-dessus de la Terre, alors le satellite semblerait dériver un peu dans le ciel, et ça ne fonctionnerait plus pour la télévision. Alors les compagnies qui gardent ces satellites en orbite doivent constamment les surveiller pour s’assurer qu’ils demeurent exactement à la bonne hauteur et à la bonne vitesse dans leurs orbites.
Un satellite qui effectue son orbite à une hauteur qui permet de faire une orbite exactement en même temps que le corps (la Terre) autour duquel il tourne se trouve dans ce qu’on appelle une orbite « géosynchrone ». Ce mot fait du sens, car la période orbitale du satellite et de la période rotationnelle de la Terre sont synchronisées.
Il s’avère que les seules choses qui importent dans le calcul de la bonne hauteur pour qu’un satellite reste géosynchrone sont la masse et la période de rotation de la planète. Alors, quand vous cochez la case pour calculer l’orbite géostationnaire, le satellite se déplace immédiatement à la bonne hauteur en se basant sur les réglages des autres curseurs. Vous ne serez pas en mesure de changer cette hauteur jusqu’à ce que vous décochiez cette case.
AVERTISSEMENT : Disons que vous gardez la période rotationnelle de la Terre à 24 heures. Il est alors possible de rendre le rayon de la Terre si grand qu’il dépassera le satellite qui tente de rester dans une orbite géosynchrone! Ça va arriver si vous n’augmentez pas la masse de la Terre pour qu’elle soit proportionnelle à sa taille plus grande. Il est impossible d’obtenir une orbite géosynchrone autour d’un corps qui aurait ainsi une très faible densité, car l’orbite devrait alors se retrouver À L’INTÉRIEUR de la planète! (Quelle devrait être la densité de la planète pour que ça arrive? Environ 1/3 de la densité du bois de balsa – alors il est très peu probable qu’on puisse avoir une planète comme ça, mais il est amusant d’y penser!)
Renseignements complets : Vous pouvez contourner tout ceci assez finalement, en ralentissant tout simplement la rotation de la planète. Mais ce n’est pas aussi amusant.
Géosynchrone vs Géostationnaire
On a utilisé le mot « géosynchrone » plus tôt, mais cela ne sert pas à grand-chose de synchroniser le satellite et la Terre ensemble si nous ne tenons pas compte du fait que notre antenne satellite sur la Terre ne bouge jamais. Plusieurs orbites qui sont géosynchrones impliqueraient qu’un satellite orbite à un angle par rapport à l’équateur, ce qui donne l’impression qu’il se déplace dans le ciel selon une ligne nord-sud. Ça ne fonctionnerait pas du tout. Alors, on utilise le mot « géostationnaire » pour décrire une orbite géosynchrone qui se trouve directement au-dessus de l’équateur – une dans laquelle le satellite ne se déplace jamais au nord ou au sud alors qu’il effectue son orbite. C’est la seule manière de s’assurer que le satellite ne semble jamais se déplacer dans notre ciel depuis la Terre.
[On devrait aussi noter que pour qu’une orbite géosynchrone puisse se retrouver en angle par rapport à l’équateur, alors l’orbite doit être elliptique pour que la vitesse du satellite soit la plus lente aux points de son orbite qui sont les plus éloignés de l’équateur. (On avait parlé un peu de la même chose avec l’analemme, où le mouvement apparent du Soleil parallèle à l’équateur est plus grand quand sa déclinaison est aux points le plus élevé et le plus bas pour l’année. Ça a généré la portion « obliquité » de l’équation du temps, et c’est la raison pour laquelle la vitesse de notre satellite doit changer lors de son orbite.)]
Vu qu’un satellite géostationnaire doit faire son orbite au-dessus de l’équateur, et vu qu’il doit faire son orbite à une hauteur donnée, quelque chose d’intéressant va se passer pour toutes les personnes qui ont des antennes dirigées vers ce satellite. Plus l’antenne est située au sud sur la Terre, plus haut dans le ciel le satellite semblera être. Ça veut dire que les antennes seront plus inclinées et seront pointées plus vers le haut. Les antennes situées à une latitude plus au nord seront dirigées vers un point plus bas du ciel. Cet effet survient pour la même raison que le Soleil semble être plus haut ou plus bas dans le ciel pour un jour donné pour des observateurs se situant à différentes latitudes – comme on l’a vu au tout début dans le diagramme 1.
En fait, vous pourriez calculer la latitude à laquelle est installée une antenne satellite. Il suffit de connaître l’angle entre l’antenne et le sol! (Vous devriez aussi connaître la différence en longitude entre l’antenne et le point sub-orbital du satellite – mais ce sera pour une autre discussion!)
Ce que vous pouvez apprendre :
- Ce qui permet à un objet d’effectuer une orbite autour d’un corps plus grand
- Comment la masse du corps plus grand affecte la hauteur et la vitesse d’un objet en orbite
- Ce que sont les orbites géosynchrones et géostationnaires, et comment elles sont utilisées
- Pourquoi l’antenne satellite sur votre maison n’a jamais besoin de bouger
Magnitudes des étoiles
Comment les astronomes décrivent-ils la luminosité des étoiles?
Consultez les instructions du diagramme 28Refermer les instructions
Diagramme 28 :
Magnitudes des étoiles
Ce que vous regardez :
Lorsque le diagramme se charge, vous voyez deux étoiles. Chacune d’elle a sa propre barre de défilement pour contrôler son niveau de luminosité. On vous montre la luminosité selon la taille de l’étoile, ainsi qu’un nombre appelé « magnitude ». On vous montre aussi comment une étoile est plus brillante qu’une autre, en se basant sur les valeurs que vous sélectionnez pour chacune d’entre elles.
Lisez plus à propos de la magnitude des étoiles et leur luminosité dans la leçon ci-dessous!
Si vous cliquez sur le bouton en haut à droite (« Magnitude absolue »), vous irez à la partie 2 du diagramme. Ici, vous avez une étoile, et vous pouvez modifier autant sa magnitude apparente que sa distance depuis la Terre. L’étoile à la droite va vous montrer ce qu’est la « magnitude absolue ». Encore, vous voudrez lire à propos de tout ça dans la leçon ci-dessous.
Dans cette partie du diagramme, vous pouvez aussi cocher la case « Soleil ». Ça va vous montrer les valeurs fixes pour la distance et la magnitude absolue et apparente du Soleil.
Magnitudes des étoiles
Si vous regardez les étoiles dans le ciel, il est évident que certaines sont plus brillantes que d’autres. Certaines étoiles sont plus près de nous que d’autres, et certaines étoiles sont tout simplement plus grandes et brillantes que d’autres. La combinaison de la luminosité réelle de l’étoile et sa distance par rapport à nous se combine pour nous donner la luminosité telle qu’elle semble nous apparaître depuis la Terre.
Si vous preniez n’importe quelle étoile et la déplaciez plus proche de nous, alors elle deviendrait plus brillante. Si vous laissiez n’importe quelle étoile en place mais la rendiez moins « lumineuse » (une mesure de sa luminosité réelle), alors elle deviendrait plus sombre. Pour que ça fasse du sens, ceci correspond à ce qu’on peut expérimenter sur Terre avec une chandelle et une lampe de poche.
Mais comment peut-on faire pour mesurer la luminosité de chaque étoile? Et comment peut-on communiquer cette luminosité pour qu’on puisse comparer les étoiles entre elles?
La luminosité est mesurée de différentes manières en science. La quantité de lumière qui est présente est mesurée en « lumens », et le niveau de luminosité de cette lumière lorsqu’elle éclaire quelque chose est appelée éclairement lumineux. L’intensité de la lumière est mesurée en « lux ». L’intensité lumineuse est mesurée en « candelas ». Dans le système anglais, on a aussi un terme appelé « foot-candle ». (Un peu confus?) Oh, et en passant, aucune de ces unités ne serait bonne pour décrire les étoiles, parce qu’elles sont beaucoup trop grosses; nous ne voyons aucune étoile depuis la Terre qui est aussi brillante qu’une chandelle!
L’approche du gros bon sens
Les anciens astronomes voulaient une manière facile de donner un nombre simple à une étoile, pour la classer avec un groupe d’étoiles similaires ayant toutes à peu près la même luminosité. Au tout début, ils avaient seulement leurs yeux pour tenter d’effectuer ces déterminations, et cela faisait du sens qu’ils appellent les étoiles brillantes « de première magnitude », et les étoiles plus sombres « de deuxième », « de troisième », « de quatrième »magnitude, et ainsi de suite. Ce système de classification est resté avec nous jusqu’à aujourd’hui. Même maintenant, quand les astronomes peuvent mesurer de manière très précise la luminosité apparente d’une étoile, on utilise encore la « magnitude » pour décrire la luminosité d’une étoile. Nous avons aussi retenu le système dans lequel une magnitude plus grande est plus sombre qu’une avec une magnitude plus basse.
Plus près d’aujourd’hui, une formule mathématique a dû être adaptée à ces « fourchettes » de luminosité existantes, et il a été très vite déterminé qu’une fonction linéaire normale ne ferait pas l’affaire. La manière dont les humains perçoivent la luminosité relative a fait en sorte que la classification initiale des étoiles est tombée dans ce que nous appelons maintenant une échelle « logarithmique », et on devrait décrire en quoi ça consiste avant d’aller plus loin.
Il y a plusieurs choses que nous vivons dans nos vies normales qui couvrent un très large éventail de valeurs. Depuis les étoiles les plus brillantes jusqu’aux plus sombres que vous pouvez apercevoir, il existe une vaste gamme de luminosités. Depuis les sons les plus forts jusqu’aux plus faibles, encore une fois il y a une variation énorme dans l’énergie sonore qui est produite. Et aussi, depuis les plus faibles grondements de la Terre jusqu’aux séismes les plus violents, nous avons besoin d’une échelle pour mesurer l’activité géologique qui couvre une gamme très large de valeurs. Chacune de ces trois caractéristiques physiques est mesurée en termes logarithmiques.
Logarithmes?
Pour comprendre les logarithmes, vous devez comprendre les puissances. On peut prendre quelques exemples pour vous montrer comment une échelle logarithmique fonctionne.
Supposons que vous avez quatre exemples de choses qui tombent dans une des catégories mentionnées plus haut, et que vous avez les valeurs suivantes pour vos exemples :
Exemple 1: valeur = 10Exemple 2: valeur = 100
Exemple 3: valeur = 1000
Exemple 4: valeur = 10 000
Vous voulez être en mesure d’attribuer des valeurs pour d’autres mesures qui tombent entre celles-ci, pour que vous puissiez dire par exemple qu’une valeur de 20 tomberait entre l’exemple 1 et l’exemple 2 de la même manière que 2000 tomberait entre l’exemple 3 et l’exemple 4. Bien sûr, il y a une bien plus grande différence entre 1000 et 2000 qu’il y a entre 10 et 20, mais vous voulez être en mesure de dire que relativement parlant, la valeur 2000 est plus forte (ou plus lourde, ou plus brillante) que 1000 « de la même manière » que 20 est plus fort que 10. Les logarithmes sont la réponse à ce problème.
Et si vous changiez l’échelle de vos mesures pour incluse des puissances de 10 au lieu des valeurs que vous avez mesurées pour les exemples? Alors vous pourriez affirmer ce qui suit :
Exemple 1 = 10 = 101, alors on l’appelle “1”.Exemple 2 = 100 = 102, alors on l’appelle “2”.
Exemple 3 = 1000 = 103, alors on l’appelle “3”.
Exemple 4 = 10 000 = 104, alors on l’appelle “4”.
Maintenant, si un autre exemple survient avec une valeur de 20 (ce qui est 10 puissance 1,3), et qu’un autre exemple vient avec une valeur de 2000 (ce qui est 10 puissance 3,3), vous pouvez voir que cette puissance supplémentaire de 0,3 est la même pour vos deux nouvelles valeurs! On a trouvé un moyen de relayer la relation que nous voulions, en utilisant tout simplement des puissances de 10! Ces deux exemples sont à peu près « 0,3 de plus que » (ou « 0,7 de moins que ») un des exemples avec lesquels nous avons débuté.
Plus tôt, on a utilisé le mot « logarithme » (ou l’abbréviation « log ») parce que log est l’opposé mathématique de puissance. (Techniquement, c’est appelée une fonction « inverse », mais on va juste utiliser le mot « opposé »). Si vous voulez savoir quelle puissance de 10 est représentée par le nombre 20, vous pouvez utiliser la fonction log puis entrer le nombre 20 sur votre calculatrice scientifique et vous l’aurez. (En fait, c’est assez près de 1,3)
On va à présent décider qu’on va décrire nos exemples en utilisant le log, ou puissance, au lieu de la valeur réelle. Ça veut dire que si vous avez quelque chose qui est « 4 » sur cette échelle, et que j’ai un « 5 », alors votre valeur est 10 fois plus/moins brillante, ou plus/moins lourde, ou plus/moins forte que la mienne. On doit tout simplement se rappeler que chaque fois qu’on monte de 1 sur cette échelle, en fait on multiplie la valeur précédente par 10.
Et la vraie beauté de ça est que nous n’avons pas besoin d’utiliser 10 comme base du log. On peut utiliser n’importe quel nombre, aussi longtemps que les résultats tombent dans la gamme de valeurs dont on veut parler – comme la gamme de luminosité des étoiles dans le ciel. Par contre, pour les « magnitudes » des étoiles, si une valeur de la cinquième racine de 100 est choisie comme base, alors les choses se mettent bien en place.
Mais qu’est-ce que c’est que la cinquième racine de 100? À peu près deux et demi. Alors, si vous regardez deux étoiles, et qu’une d’elles est de magnitude 3 alors que l’autre est de magnitude 4, ça veut dire qu’une d’elles est 2,5 fois plus brillante que l’autre. Ça demeure aussi vrai si vous parlez des magnitudes 10 et 11, 2 et 3, 0 et -1, etc. L’étoile plus lumineuse est 2,5 fois plus brillante que l’étoile plus sombre.
Mais laquelle est la plus brillante? Rappelez-vous, plus la magnitude est petite, plus l’étoile est brillante. Ça correspond à la vieille classification où les étoiles les plus brillantes étaient dans la « première » magnitude, et les plus sombres étaient étiquetées « deuxième » ou « troisième » classe, etc. Alors, la magnitude 3 est plus brillante que la 4. Une magnitude de 0 est plus sombre que -1, et ainsi de suite.
En utilisant cette échelle, ça fait maintenant du sens de parler de magnitudes qui sont tellement peu brillantes qu’on ne peut même pas voir l’étoile. Si une étoile est plus sombre que magnitude 6, vous ne pourrez pas la voir, peu importe à quel point votre ciel est sombre. Avec un télescope, vous pourriez être en mesure de voir les étoiles de la 9e, 10e ou 11e magnitude. Le télescope spatial Hubble permet de voir des étoiles de la 31e magnitude – quasiment dix mille millions de fois plus sombres que les étoiles qu’on peut à peine apercevoir depuis la Terre! (Et il est beaucoup plus facile de parler de nombres comme 6 et 31 que de nombres comme 10 milliards!)
En utilisant cette échelle, on peut aussi parler des magnitudes qui sont fractionnelles. Ça veut dire qu’on peut affirmer qu’une étoile A a une magnitude de 2,34, alors qu’une étoile B a une magnitude de 2,41. Dans ce cas, l’étoile B sera juste un tout petit peu plus sombre que l’étoile A. Une fois qu’on a internalisé ce système, ce n’est pas très important que l’étoile B soit 7,6% plus sombre que l’étoile A (à moins qu’on fasse une expérience qui nécessite cette information). Ce qui nous préoccupe, c’est que l’étoile A est « un tout petit peu » plus brillante que la B, et que c’est difficile de voir la différence juste en les regardant.
Ça fait aussi du sens de parler des étoiles avec une magnitude 0, ou même de celles avec une magnitude négative! L’étoile la plus brillante dans le ciel (appelée « Sirius ») a une magnitude de -1,46. Sa plus proche rivale est Canopus avec une magnitude de -0,74, mais Canopus n’est pas visible depuis la plus grande partie de l’Europe et des États-Unis, et elle n’est pas du tout visible depuis le Canada.
Il y a présentement seulement 16 étoiles plus brillantes que la magnitude 1,0, et seulement quatre qui sont plus brillantes que la magnitude 0,0. (Si on ne compte pas le Soleil – qui vient avec une magnitude impressionnante de -26,7!) Si vous voulez voir un bel exemple d’une étoile avec une magnitude 0 (et que vous êtes dans l’hémisphère Nord), alors vous pouvez trouver l’étoile Vega, qui fait partie de la constellation de la Lyre. Elle fait aussi partie du « Triangle d’été » - un ensemble de trois étoiles (avec Deneb et Altair) qui forment un très large triangle qui se retrouve au-dessus de nos têtes pendant l’été dans l’hémisphère Nord. La magnitude de Vega est de 0,026 – très près de zéro!
Cette échelle logarithmique pour la magnitude permet de se faire très facilement une idée de la luminosité d’une étoile, sans avoir recours aux mathématiques ou à la physique. C’est pourquoi on s’en sert tout le temps pour parler de la luminosité des étoiles.
Aussi, rappelez-vous quand on a parlé plus tôt des séismes et des sons. Et bien, l’échelle des décibels qu’on utilise pour parler du niveau de bruit est logarithmique. L’échelle de Richter qu’on utilise pour parler de la force d’un séisme est aussi logarithmique. Ces logarithmes sont très utiles!
Magnitude absolue
Si vous cherchez les étoiles dans un catalogue d’étoiles, vous verrez habituellement apparaître deux magnitudes : la magnitude « apparente » et la magnitude « absolue ». La magnitude apparente est une mesure de la luminosité apparente d’une étoile telle que vous pouvez la voir quand vous regardez cette étoile. Mais rappelez-vous, la luminosité apparente d’une étoile peut être très différente de sa luminosité réelle. Il y a certaines étoiles qui sont incroyablement brillantes, mais elles sont tellement loin de nous qu’elles semblent plutôt sombres à partir de la Terre. Et il y a des étoiles (comme notre Soleil) qui semblent TRÈS brillantes – mais si vous les placiez à la même distance que la plupart des autres étoiles, elles sembleraient plutôt ordinaires. Le mot technique qu’on a besoin encore une fois ici est « luminosité ». Une étoile qui a une plus grande « luminosité » qu’une autre étoile serait plus brillante si vous placiez les deux étoiles à la même distance depuis la Terre.
Pour aider à comparer des étoiles en retirant le facteur de la distance, les astronomes ont inventé le terme « magnitude absolue » pour mettre toutes les étoiles au même niveau et pour nous dire à quel point une étoile serait brillante si on pouvait la placer à une distance prédéterminée de la Terre. Cette distance prédéterminée a été établie à 10 parsecs, ou 32,6 années-lumières.
Vous pouvez utiliser la magnitude absolue pour comparer la luminosité réelle des étoiles, mais vous devrez chercher les valeurs dans un tableau. Et rappelez-vous, si l’étoile est en fait plus près de nous que 32,6 années-lumières, sa magnitude absolue sera plus sombre que sa magnitude apparente! (C’est parce que pour obtenir la magnitude absolue, on devrait déplacer l’étoile plus loin de la Terre qu’elle ne l’est réellement!) Il y a quelques étoiles dans le ciel que vous ne pouvez même pas apercevoir à l’oeil nu, mais qui seraient aussi brillantes que la pleine Lune si elles étaient placées aussi près qu’à 10 parsecs de nous. Même des étoiles célèbres comme Bételgeuse, Antarès et Deneb deviendraient spectaculairement brillantes à cette distance. Mais notre Soleil? Il brillerait à une magnitude de 4,8, ce qui veut dire que vous auriez besoin d’un ciel très sombre pour pouvoir même être en mesure de le trouver. Il disparaîtrait littéralement dans une mer de milliers d’autres étoiles plus pâles que la moyenne. C’est quelque chose qui porte à réflexion!
La magnitude absolue est vraiment une notion académique, parce qu’il est impossible que les étoiles pourront toutes magiquement se placer à une distance de 10 parsecs de la Terre. Mais c’est une très bonne manière de comparer leur luminosité relative. Vous devez juste vous rappeler que la luminosité apparente d’une étoile dépend grandement de sa luminosité réelle ET de sa distance depuis la Terre.
Oh, et si vous vous demandiez comment les astronomes savent quelle est la luminosité réelle d’une étoile, il y a plusieurs manières. Ça sort du cadre de cette leçon de vous donner toutes les méthodes (incluant la spectroscopie, le mouvement propre, le placement dans la séquence principale, le décalage vers le rouge, et plusieurs autres), mais il suffit d’affirmer que si vous voulez étudier les étoiles pour voir à quel point les mesures des scientifiques peuvent être précises, il y a plusieurs informations qui vous attendent et que vous pouvez découvrir. Peut-être que vous voudrez même poursuivre des études formelles en astronomie, et vous pourrez contribuer aux prochaines grandes découvertes!
Ce que vous pouvez apprendre :
- Vous pouvez apprendre à propos des logarithmes et des échelles logarithmiques.
- Vous pouvez apprendre à propos de différentes choses qu’on mesure dans la vie de tous les jours et qui sont logarithmiques.
- Vous pouvez voir comment la luminosité d’une étoile et sa distance influencent sa luminosité depuis la Terre.
- Vous pouvez apprendre comment un grand nombre pour la magnitude représente une étoile plus pâle.
- Vous pouvez apprendre à propos de l’invention que les astronomes utilisent (« magnitude absolue ») pour comparer facilement la luminosité des étoiles.
L’alphabet grec
Apprendre les lettres grecques! Vous en aurez de besoin en astronomie.
Consultez les instructions du diagramme 27Refermer les instructions
Diagramme 27 :
L’alphabet grec
Il est important de connaître les lettres grecques, si vous voulez étudier les mathématiques et la physique – mais vous devrez aussi les connaître pour l’astronomie! Nous aborderons plus ce sujet dans le diagramme sur les Désignations des Étoiles, mais pour l’instant, nous allons vous fournir une méthode facile pour étudier les lettres grecques.
Ce que vous regardez :
Dans ce diagramme, nous vous offrons une méthode facile pour apprendre les lettres grecques. Faites tout simplement glisser la bannière pour n’importe quelle lettre, et une grille vous montrera la lettre. Vous verrez chaque lettre affichée avec quatre polices de caractère différentes mais très communes. Ça vous aidera à reconnaître les différences entre les versions standard de chaque lettre.
Notez que trois lettres ont de multiples formes de minuscules. Pour ces lettres (Thêta, Sigma et Phi), nous avons montré deux de ces formes.
Dans le cas où vous voudriez dessiner les lettres, nous avons donné quelques notes au bas de la grille à propos de choses auxquelles vous devez porter attention. Ça vous aidera à éviter des erreurs fréquentes que les élèves font lorsqu’ils écrivent les lettres.
Mode quiz
Vous pouvez aussi entrer le mode quiz, où nous vous présentons une offre aléatoire de lettres majuscules ou minuscules (à votre choix), et vous devez les nommer! Ce quiz va passer aléatoirement à travers l’alphabet complet, vous offrant l’opportunité de voir chaque lettre. À la fin du quiz (une fois que vous aurez passé à travers les 24 lettres), vous verrez un tableau avec vos résultats.
Votre but ultime devrait être de pouvoir identifier chaque lettre majuscule et minuscule à partir de son image, d’être en mesure d’écrire chaque lettre majuscule et minuscule, et de pouvoir réciter l’alphabet du début jusqu’à la fin. Quand vous pourrez faire tout ça, vous pourrez dire avec confiance que vous CONNAISSEZ le très important alphabet grec!
Ce que vous pouvez apprendre :
- L’alphabet grec!
Désignations des étoiles
Apprenez comment les lettres grecques sont utilisées pour nommer les étoiles.
Consultez les instructions du diagramme 26Refermer les instructions
Diagramme 26 :
Désignations des étoiles
Ce que vous regardez :
On vous a donné quatre constellations (quoique la Grande Ourse est plus proprement appelée un "astérisme") et on a étiqueté les étoiles principales dans chacune avec la lettre grecque les désignant. Vous pouvez cliquer sur n'importe quelle étoile pour voir plus d'informations à propos de celle-ci.
Un peu de contexte :
À présent, vous devriez savoir pourquoi vous devez connaître l’alphabet grec. Si quelqu’un vous parle de α Leo, il vaudrait mieux savoir que cette lettre grecque est un Alpha minuscule! Et ainsi de suite. Vous devez connaître les lettres pour être en mesure de lire un atlas des étoiles! Vous devez aussi connaître l’ordre des lettres dans l’alphabet grec, pour que vous puissiez savoir quelles étoiles sont plus brillantes que les autres – par exemple, Epsilon vient après Delta. Dans tous les cas, faites en sorte de connaître l’alphabet grec, pour que ne soyez pas pris au dépourvu et prononciez par erreur ν Aurigae comme un “v” (c’est “nu”) ou υ Piscium comme un “u” (c’est “upsilon”)!
Un peu de linguistique :
Qu’est-ce qu’on doit savoir à propos des mots « Leonis », « Aurigae » et « Piscium »? Les noms des constellations ne sont-ils pas « Lion », « Cocher » et « Poisson »?
Oui, c’est bel et bien le cas, mais il a été décidé très tôt que les astronomes nommeraient les étoiles en utilisant la lettre grecque (ou un nombre, ou une lettre latine, alors que d’autres catalogues ont été ajoutés) ensemble avec le génitif latin du nom de la constellation. Ça veut dire qu’au lieu de dire « L’étoile Alpha d’Orion », on dirait plutôt « Alpha Orionis ». Pour ceux d’entre vous qui ont étudié le Finnois, l’Allemand, le Russie, le Basque, le Turc, le Latin, le Grec, le Hongrois, l’Albanais, le Tchèque, le Slovaque, le Tamil ou l’Arabe, ou n’importe quelle autre langue qui utilise des génitifs, vous savez que ça représente la signification d’« avoir ». (L’anglais et les langues romanes [sauf le Roumain] utilisent des prépositions au lieu de terminaisons pour marquer la possession). Alors, quand on dit « Alpha Orionis », on dit en fait « l’étoile Alpha appartenant à Orion ». « Orionis » veut dire « d’Orion », ou « appartenant à Orion », alors c’est ce qui a été utilisé quand les désignations d’étoiles ont été déterminées.
Bien sûr, ça veut dire que vous devez apprendre le génitif latin de chacun des 88 noms de constellations. Par contre, ne nous blâmez pas pour tout ce travail supplémentaire : nous n’avons pas inventé ce système; nous vous expliquons comment l’utiliser!
(Par ailleurs, vous devez aussi connaître les abréviations des noms des constellations, pour que quand vous lisez que l’étoile ε Cnc fait partie de l’amas ouvert de la constellation du Cancer [ou M44], vous saurez que vous devez prononcer « Epsilon Cancri ».)
En théorie, vous pourriez consulter un tableau de tous les noms d’étoiles avec leurs lettres grecques, et connaître leur ordre de luminosité. Ce serait fantastique, mais ça ne se passe pas toujours comme ça. En fait, pour des raisons historiques, les deux étoiles les plus brillantes d’Orion et du Gémeaux ne sont pas nommées en ordre de luminosité. C’est vrai : Alpha Geminorum [Castor] est actuellement moins brillantes que Beta Geminorum [Pollux]! (Et c’est vrai – le génitif latin de « Gémeaux » est en fait « Geminorum ». Encore une fois, nous sommes désolés – mais vous vous y habituerez… éventuellement.)
Finalement, vous pourriez avoir remarqué qu’on utilise toujours des lettres grecques minuscules pour les noms des étoiles. C’est vrai, mais ça ne veut pas dire que vous ne devriez pas aussi apprendre les lettres majuscules. Elles sont utilisées en mathématiques et en physique – tout comme les noms des fraternités et sororités que vous retrouverez près de certains campus universitaires. Svp allez consulter le diagramme sur les lettres grecques pour vous aider à les apprendre.
Vous pourrez ensuite revenir à ce diagramme et voir trois autres constellations, pour vous montrer comment les lettres grecques sont utilisées pour leurs étoiles.
(Dans un diagramme à venir, on va vous montrer toutes les constellations, et vous donner l’opportunité d’apprendre leurs étoiles, leurs abréviations et les formes génitives de leurs noms!)
Ce que vous pouvez apprendre :
- Vous apprendre comment les désignations primaires des étoiles brillantes dans chaque constellation ont été assignées.
- Vous verrez que ces désignations vous donneront une bonne idée de l’ordre de luminosité des étoiles dans chaque constellation.
- Vous pouvez apprendre qu’il y a d’autres désignations d’étoiles aussi – particulièrement pour les moins brillantes.
- Vous pouvez apprendre que ce représente le génitif en linguistique.
- Vous pouvez voir toutes les choses que vous devrez apprendre, si vous voulez connaître les étoiles et les constellations!
Les constellations
Informations à propos de toutes les constellations dans le ciel!
Consultez les instructions du diagramme 29Refermer les instructions
Summmary
Some instructions for diagram29 in french
Sliders
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt
Le drapeau du Brésil
Apprenez les états du Brésil, et les étoiles qui leur correspondent sur le drapeau du pays.
Consultez les instructions du diagramme 30Refermer les instructions
Diagramme 30 :
Le drapeau du Brésil
Ce que vous regardez :
Vous voyez une bannière, une carte et un drapeau. La bannière en haut du diagramme contient les noms de tous les états et territoires du Brésil. Tout ceci est synchronisé ensemble pour que vous puissiez voir les relations entre les états et les étoiles qui les représentent sur le drapeau.
Contrôles :
Vous pouvez utiliser votre souris pour faire dérouler la bannière en haut, et faire glisser le curseur de la souris au-dessus des noms pour mettre en évidence cet état sur la carte et son étoile sur le drapeau.
Vous pouvez aussi déplacer votre souris au-dessus des étoiles sur le drapeau, ou des états sur la carte. Les autres éléments du diagramme vont changer pour correspondre à votre sélection.
Contexte :
Le drapeau du Brésil est unique dans le monde, car il montre une VRAIE carte d’étoiles! Plusieurs des drapeaux d’autres pays montrent des constellations et des étoiles individuelles, mais le drapeau du Brésil est tel qu’il définit un ensemble complet d’étoiles et de constellations, d’une manière représentative de leurs véritables positions dans le ciel. En fait, chaque étoile du drapeau brésilien représente aussi un des états du Brésil. Les spécifications du design du drapeau font en sorte que s’il y a un changement dans la liste des états, alors le drapeau doit être modifié en conséquence. C’est arrivé trois fois depuis la conception du drapeau en 1889 – en 1960, en 1968 et en 1992.
Ce diagramme vous montre les 27 étoiles qui sont présentement (depuis 1992) représentées sur le drapeau du Brésil. La première chose que vous pourriez remarquer est que la carte complète des étoiles apparaît à l’envers par rapport à ce à quoi elle ressemble dans le ciel. (Vous pouvez regarder la représentation de la Croix du Sud comme preuve). Ce n’est pas une erreur! Les concepteurs du drapeau ont choisi de représenter les étoiles sur le drapeau comme elles apparaîtraient si vous étiez à une distance infinie de la Terre, regardant les étoiles comme si vous étiez « au-dessus » d’elles.
Il y a un précédent historique qui permet de représenter les étoiles de cette manière. Les concepteurs du drapeau ont copié un format très ancien et respecté utilisé pour cartographier les étoiles et qui est connu comme étant une sphère « armillaire », et ce drapeau représente cet historique.
Parce que le drapeau du Brésil représente une carte des étoiles assez précise, vous devrez faire attention si vous tentez de le dessiner : chacune des positions des étoiles est établie selon des spécifications légales, et même la taille de chaque étoile doit être correcte si votre dessin doit être précis.
Les Brésiliens apprécieront vraiment chaque effort que vous faites pour vous assurer que vous avez élaboré votre version de leur drapeau d’une manière aussi représentative possible de l’original. Bien sûr, les scientifiques feront de même, car il ne fait aucun doute que la conception soignée de ce drapeau suscite l’admiration et le respect des astronomes du monde entier!
Une note spéciale :
La très petite étoile au milieu en bas de la partie bleue du drapeau est Sigma Octantis. Cette étoile est très pâle, mais aussi très spéciale. Alors que l’hémisphère nord a une étoile brillante située très près de son pole, il n’y a présentement pas d’étoile brillante qui peut servir d’étoile pour le Pôle Sud.
Sigma Octantis est l’étoile visible la près du pôle sud céleste – bien qu’il faille un ciel sombre pour la voir! Même à ça, parce que Sigma Octantis occupe cet emplacement spécial dans le ciel, les Brésiliens l’ont choisie pour représenter le district fédéral où se trouve leur capitale, Brasilia. L’« étoile polaire » - la base du ciel méridional – représente donc l’endroit où siège le gouvernement du Brésil!
Ce que vous pouvez apprendre :
- Vous pouvez apprendre comment le drapeau du Brésil contient des étoiles qui correspondent avec chaque état.
- Vous pouvez apprendre les emplacements et les noms des états se trouvant au Brésil.
La Force Gravitationnelle
Découvrez la force gravitationnelle entre deux objets.
Consultez les instructions du diagramme 31Refermer les instructions
Diagramme 31 :
La force gravitationnelle
Ce diagramme présente trois scénarios qui peuvent vous aider à en apprendre davantage sur la force gravitationnelle.
La gravitation est une force qui s’exerce sur tous les objets de l'univers. C'est la force qui nous retient sur la Terre et qui fait que les objets tombent quand on les lâche. On pense souvent que la force gravitationnelle est TRÈS forte, mais en fait il s’agit d’une des forces les moins puissantes dans la nature. Les objets doivent avoir une TRÈS grande masse pour que leur force d’attraction ait un effet sur d’autres objets.
Dans ce diagramme, nous allons nous intéresser uniquement à la force qui s’exerce entre deux objets. Bien sûr, si vous avez plus de deux objets, ils s’attireront tous mutuellement. Une situation comme ça devient vite compliquée, alors nous allons nous limiter à un système à deux objets. (En fait, si vous avez trois corps célestes ou plus, il faut généralement recourir à des calculs extrêmement compliqués, voire à une simulation informatique, pour savoir comment ils vont se déplacer et s'attirer les uns les autres).
Nous allons ajouter des chiffres dans une équation, et voir à quoi ressemble la « force » que nous obtenons en résultat. Le but de ce diagramme est de réussir à calculer cette force. C'est un nombre qui nous indique la force avec laquelle nos deux objets s’attirent mutuellement. Si la force est suffisamment puissante, les deux objets s’attirent tellement qu'ils vont se déplacer ensemble, orbiter l'un autour de l'autre, ou même se coller l'un à l'autre. C’est ce qui se passe quand vous échappez un objet ; la Terre l’attire et il tombe au sol. En fait, la Terre et l'objet que vous avez laissé tomber se rejoignent dans l'espace. La distance que chaque objet doit parcourir à la rencontre de l'autre est basée sur leur taille relative. Ça veut dire que le petit objet qui a glissé de votre main bouge beaucoup plus que la Terre! Nous percevons ce mouvement comme une « chute ».
De même, en vous tenant debout, immobile, vous pouvez ressentir la force d’attraction de la Terre qui vous tire vers le bas. Vous ressentez cette force comme une pesanteur qui vous cloue au sol, et la seule raison pour laquelle vous ne continuez pas à tomber jusqu’au centre de la Terre c’est que le sol ou le plancher vous arrête!
Nous allons partager avec vous une seule formule mathématique, mais c’est une formule TRÈS importante. La voici :
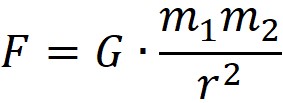
Décortiquons un peu cette formule :
F est la force que nous essayons de calculer. C'est la « puissance d'attraction » qui existe entre les deux objets.
Les masses de nos deux objets correspondent à m1 et m2. Si vous n'avez pas encore étudié la physique, imaginez que la masse et le poids sont plus ou moins la même chose. Ce n’est pas du tout le cas dans la vraie vie, mais pour les besoins de cet exercice, on peut imaginer qu'ils le sont. La masse, c'est la quantité de « matière » contenue dans un objet. Un ballon n'est donc pas très massif parce qu'il est rempli de choses très légères : de l'air ou de l'hélium, par exemple. Un bloc de plomb de la même taille que ce ballon sera aura une masse beaucoup plus grande. Un objet de la taille de la Terre est vraiment massif, et le Soleil a une masse encore plus grande que celle de la Terre. Ce concept nous aidera à comprendre la force gravitationnelle.
La distance entre nos deux objets est r. Pourquoi utiliser « r » pour la distance? Eh bien, en physique, c’est parfois très utile de visualiser un cercle ou une sphère avec un objet au centre et l'autre objet à l'extrémité du rayon de cette sphère. Cette méthode facilite les calculs mathématiques. Ici, « r » signifie « rayon ». Si vous préférez l'appeler « d », pas de problème, mais la formule est généralement donnée avec la lettre r.
G est un nombre très spécial. On l'appelle la « constante gravitationnelle », et ça décrit bien de quoi il s’agit : une constante qui a été mesurée avec une grande précision, et qui est très stable sur les distances et dans le temps. En d'autres termes, la science actuelle pense que G est constant maintenant, qu'il l'a toujours été et le sera toujours. Ce n’est pas prouvé hors de tout doute, mais dans le cadre de nos expériences en classe, nous pouvons supposer que G est constant. Il n’y a pas non plus de raison de croire que G n'est pas constant partout dans l'univers.
(Au cas où ça vous intéresse, G est égal à 6,67408 × 10-11 m3 kg-1 s-2. Mais nous avons promis que vous n’auriez qu’une seule formule à apprendre, et ça ressemble VRAIMENT trop à une formule mathématique. Alors pour l’instant, ne vous préoccupez pas de ça!)
Retournons à la formule de la force gravitationnelle. Vous vous rappelez à quoi elle ressemble :
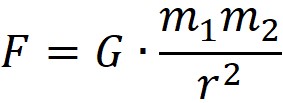
Si on lit cette formule en français, voici ce qu’elle veut dire :
« La force gravitationnelle entre deux objets est proportionnelle à leurs masses, et inversement proportionnelle au carré de la distance qui les sépare. »
Mmm. Cela ressemble encore beaucoup trop à des mathématiques. En français plus simple, voilà ce que ça veut dire :
« Plus deux objets sont massifs, plus la force gravitationnelle qui s’exerce entre eux est grande. Et plus les deux objets sont proches, plus la force gravitationnelle entre eux est grande. Et la distance est beaucoup plus importante que les masses. »
Ça veut dire que la force gravitationnelle augmentera davantage si nous déplaçons les objets deux fois plus près l’un de l’autre, que si nous les rendons deux fois plus massif. Si nous faisons en sorte que les DEUX objets soient deux fois plus massifs, mais que nous les plaçons deux fois plus loin l’un de l’autre, la force restera la même. Mais pour que la force gravitationnelle reste la même, il nous a suffi de faire une modification à la distance (nous avons éloigné les objets) - alors que nous avons dû doubler les DEUX masses pour compenser cela. Voilà pourquoi en fin de compte, la distance est plus importante.
Ce que vous regardez :
Venons-en au diagramme. Vous avez le choix entre trois modes et voici une brève description de chacun :
Les gros objets :
Ici, nous utilisons trois très gros objets (le Soleil, la Lune et la Terre), et nous démontrons les forces qui s'exercent entre eux. Ces objets sont si gros que leurs masses exercent une influence malgré les énormes distances qui les séparent. Cela signifie que les forces gravitationnelles entre eux sont puissantes, et c'est pourquoi ils restent en orbite les uns autour des autres!
Petits objets :
Ici, nous avons deux objets beaucoup, beaucoup plus petits que les planètes et les étoiles. Ces objets sont d’une taille typique des objets ordinaires de votre quotidien, et vous pourrez vous amuser à changer leurs masses et leurs distances afin de calculer les (minuscules) forces gravitationnelles qui s’exercent entre eux.
Force relative :
Lorsque vous étudiez la gravitation en cours de physique, vous devrez souvent calculer quels changements la force gravitationnelle subit lorsque vous éloignez ou rapprochez des objets ou lorsque vous changez leur masse. Grâce à ce mode, vous verrez que ces problèmes mathématiques sont plus faciles que vous ne le pensiez!
Voyons maintenant quelques descriptions détaillées des trois modes dans le diagramme :
Les gros objets :
Cette image illustre seulement trois situations. Vous pouvez sélectionner le système Terre-Soleil, le système Terre-Lune ou le système Soleil-Lune. Dans chaque cas, vous verrez que les forces entre les deux énormes objets sont elles-mêmes très importantes. Les chiffres apparaissent en notation scientifique, vous devrez donc comprendre ce système pour pouvoir lire et comparer les nombres. Mais croyez-nous sur parole - les forces sont TRÈS importantes!
Voici un fait très intéressant. Tout d'abord, sélectionnez le système Terre-Lune, et remarquez l'épaisseur de la flèche qui les relie. Ensuite, sélectionnez le système Soleil-Lune et comparez l’épaisseur de sa flèche. Vous verrez que la force gravitationnelle entre le Soleil et la Lune est plus grande que la force entre la Terre et la Lune. C'est exact - le Soleil tire sur la Lune plus fort que la Terre! Les astronomes disent souvent que la Lune tourne en fait autour du Soleil, et que le rôle de la Terre est seulement de la faire vaciller pendant qu’elle orbite. C’est la raison pour laquelle ils peuvent dire ça!
Petits objets :
Ici, vous avez beaucoup plus de contrôle sur les objets du diagramme. Voici deux objets dont la masse peut varier de 1 kg (environ le poids d’un litre d'eau, d’un ananas ou d’un régime de bananes de taille moyenne) à 10 000 kg (le poids d’une voiture blindée, de deux petits hélicoptères ou environ la moitié d'un gros autobus). La distance entre les objets peut être réglée de 1 cm à 10 m (la plus haute plate-forme de plongée aux Olympiques).
Ces réglages vous permettent d'expérimenter avec des objets ordinaires à des distances normales qui font partie de notre quotidien. Vous verrez tout de suite qu’à ces échelles, la force gravitationnelle est TRÈS faible. Par exemple, deux personnes de taille moyenne doivent se tenir à environ 1 cm de distance pour que la force entre elles soit égale à la moitié du poids d’un trombone! Et n'oubliez pas que quand on parle de distance, il faut que les centres de ces deux personnes soient à cette distance l’un de l’autre, ce qui est physiquement impossible dans la vraie vie!
En fait, il est presque impossible de positionner deux gros objets physiquement assez proches pour obtenir une force gravitationnelle égale au poids d'un capuchon de stylo. C'est pourquoi nous ne ressentons pas les effets des forces gravitationnelles sur les objets de notre vie quotidienne.
(Remarquez bien ici que nous convertissons la force - qui est calculée dans une unité de mesure appelée « Newtons » - en grammes ou kilogrammes, en prenant pour acquis que nous sommes à la surface de la Terre. C’est suffisamment précis pour vous expliquer le concept. Tu auras le plaisir de découvrir ce truc de physique quand tu étudieras la physique à l'école)!
Force relative :
Lorsque vous apprendrez la force gravitationnelle à l’école, le professeur vous posera souvent des questions comme celle-ci (surtout dans un examen!) :
« Supposons que vous avez deux objets. Vous triplez la distance entre eux. Ensuite, vous rendez l'un des deux objets quatre fois plus massif, et vous réduisez la masse de l’autre objet de moitié. Quel est l'effet net sur la force gravitationnelle entre les deux objets? »
Ce problème semble très compliqué jusqu'à ce que vous vous rappeliez la formule. Si les masses changent, la force changera en même temps qu'elles. Ça veut dire que si vous avez quadruplé une masse et réduit l'autre de moitié, alors le changement de votre force gravitationnelle est de 4*(1/2) – ce qui signifie que vous l'avez en fait doublée. Ensuite, vous réalisez qu'en triplant la distance, votre nouvelle force a diminué du carré de 3, soit 9. Il suffit donc de prendre notre force « doublée » et de la diviser par 9, pour obtenir une nouvelle force gravitationnelle finale équivalente aux 2/9 de la force qui s’exerçait avant.
C'est le changement d'une masse, multiplié par le changement de l'autre masse, divisé par le carré du changement de la distance – exactement comme le dit la formule! (Et si vous vous demandez ce que deviennent les G de la formule, ce nombre est une constante ; il ne change pas! Ça veut dire qu'il n'affecte pas la variation de la force.)
Dans le diagramme, vous pouvez régler les curseurs comme vous le souhaitez, et les nouveaux nombres s’afficheront dans la formule ainsi que dans la réponse finale qui sera calculée pour vous.
Bonne chance pour votre examen !
Quelque chose de plus :
Comme vous le voyez dans la formule de la force gravitationnelle, lorsque la distance entre les objets augmente, la puissance de la force est divisée par le carré de toute augmentation de la distance, et lorsque la distance diminue, la force est multipliée par le carré de la diminution de la distance. En physique, cette règle est connue sous le nom de loi de « l’inverse du carré ». Cette situation mérite bien son propre nom car il existe de nombreuses autres situations en physique qui obéissent aussi à une loi de « l'inverse du carré ». La quantité d'énergie reçue d'une source lumineuse obéit à une loi de l'inverse du carré. C’est aussi le cas pour l'énergie radar, l'interaction entre les particules chargées et le niveau de pression acoustique. Ce ne sont que quelques exemples d'application de cette loi de l'inverse du carré. Elle est très importante en physique, et surtout dans un concept aussi fondamental que la force gravitationnelle.
Ce que vous pouvez apprendre :
- De nombreuses quantités en physique, y compris la force gravitationnelle, obéissent à la loi de l’inverse du carré.
- La force gravitationnelle classique est basée UNIQUEMENT sur les masses des objets et la distance entre eux.
- On pense que la constante gravitationnelle est universelle à travers l'espace et le temps.
- La distance est très importante, mais les grandes masses font aussi une différence!
- La force gravitationnelle n'est vraiment applicable qu'à l'échelle des corps célestes énormes du système solaire ou de l'univers.
- La force gravitationnelle dépend de la distance entre les centres des corps concernés. (Ce sera très important dans votre cours de physique!)
- La force gravitationnelle qui s’exerce entre trois corps célestes ou plus est beaucoup plus compliquée que ce qu’un simple modèle peut démontrer
Notation Scientifique
Apprenez comment écrire les nombres dans un langage scientifique.
Consultez les instructions du diagramme 32Refermer les instructions
Diagramme 32 :
Notation scientifique
En astronomie, nous utilisons tout le temps de très grands nombres. Vitesses, distances, orbites, masses - tout est grand. En fait, ils sont « astronomiquement » grands! Et lorsqu’on combine l'astronomie à d'autres sciences, comme la physique et la chimie, on a aussi besoin d’utiliser de très petits nombres. Les longueurs d'onde de la lumière, la microgravité autour des petits astéroïdes, les atomes et les molécules qui composent tous les éléments de l'univers – ils sont tous décrit par des nombres qui peuvent être très petits.
Les nombres peuvent comporter beaucoup de zéros
45 000 000 000? 0,000000364? Les scientifiques trouvent que c’est ennuyeux d'écrire tout le temps de très petits et très grands nombres, ils ont donc trouvé un moyen d'éviter d'écrire tous ces zéros. Nous utilisons leur méthode dans beaucoup de nos diagrammes, nous devons donc vous expliquer ce que vous allez y voir.
Pourquoi ne pas simplement utiliser des noms?
Les grands et les petits nombres peuvent s'écrire avec des puissances de dix, et c’est une méthode assez simple à comprendre. Disons que vous avez un nombre comme 1 milliard : 1 000 000 000. Ça fait beaucoup de zéros, et c’est tentant d’écrire le nombre en mots plutôt qu’en chiffres. Mais le mot « milliard » ne signifie pas nécessairement la même chose dans tous les pays. Ce qu'on nomme un milliard dans un certain pays peut parfois s’appeler un billion dans un autre pays, et ça veut dire que nous ne pouvons pas simplement utiliser le nom du nombre.
Certains pays utilisent également leurs propres noms pour les grands nombres, ce qui ne se traduit pas toujours bien ; « Lakh » (100 000) et « Crore » (10 000 000) sont beaucoup utilisés en Asie du Sud, mais la plupart des Occidentaux n'en ont jamais entendu parler.
De plus, les noms peuvent être très trompeurs. Vous avez peut-être remarqué que tous ces millions, milliards et billions se mélangent parfois dans votre tête. Mais il y a une énorme différence entre eux - par exemple, un million de secondes correspond à environ 12 jours. Un milliard de secondes correspond à environ 31 ans. Et un billion de secondes correspond à 31 700 years. Toute une différence! Ça veut dire qu’il nous faut une façon plus précise de décrire les grands nombres, si nous voulons nous en servir pour nos calculs.
Le nombre « 1 milliard » s'écrit avec le chiffre 1 suivi de neuf zéros. Mille est un 1 avec trois zéros, et un million est un 1 avec six zéros. N’aimeriez-vous pas trouver un moyen pour ne pas devoir écrire tous ces zéros? Peut-être que si nous pouvions simplement dire combien de zéros il y a dans un nombre, ça suffirait? On comprendrait alors que, chaque fois que ce chiffre augmente d’un, disons en passant de 15 à 16 zéros, cela signifie qu’on ajoute un autre zéro au nombre. C'est la même chose que de le multiplier par 10. Et si on avait cette notation spéciale, nous pourrions l'utiliser même pour parler d'un 1 avec cent zéros derrière. Ce serait plus pratique que d'écrire 100 zéros et de s'attendre à ce que quelqu'un les compte tous sans se tromper. (« Oups, vous en avez seulement compté 99 - vous êtes décalé d'un facteur de dix! ») Cette différence pourrait être importante.
Notation scientifique
Heureusement, un tel système existe, et il s'appelle la notation scientifique. Dans la notation scientifique, nous utilisons des puissances de dix. Il s'agit simplement de décrire combien de zéros comporte le nombre dont on parle. Donc, pour 1 000, il y a trois zéros. Nous appellerons ça 103, et en fait, 103 est vraiment 1 000. C'est un 1 suivi de trois zéros.
Donc si 103 est mille, que serait un million (1 000 000)? Eh bien, un million a six zéros, donc ce serait 106. Un milliard serait 109. Un billion serait 1012, et ainsi de suite. On arrive à éviter d'écrire tous ces zéros en disant simplement 1012. C'est une belle notation compacte, et elle fonctionne très bien.
Maintenant, les nombres que vous pouvez imaginer n'ont pas toujours un 1 avec un tas de zéros après. Par exemple, disons que vous parlez de 2 billions, par exemple. Dans ce cas, vous pouvez dire 2×1012, parce que ça correspond juste à 2 fois la valeur de 1012. Avant, c'était un 1 avec 12 zéros, et donc avec deux maintenant ça fait un 2 avec 12 zéros.
Arrondir les nombres
Qu'en est-il du nombre « deux billions, 500 milliards » (2 500 000 000 000)? Il y a un 2 et un 5 dans ce chiffre, et nous devons maintenant penser un peu plus mathématiquement. Ce que nous avons vraiment, c'est un 25 avec onze zéros après, donc on pourrait dire 25×1011, et ce serait suffisant. Mais les scientifiques se sont dit que si vous essayez de faire ça avec un nombre comme 2 543 824 130 000, ça vous force à écrire un grand nombre de chiffres juste pour dire 254 382 413×104. Cette « simplification » ne sert pas à grand chose! Et tous ces petits chiffres n'ont peut-être pas d'importance pour le calcul ou l'expérience que vous faites. Les scientifiques sont donc parvenus à un accord : chaque fois que nous avons un nombre multiplié par 10 à une puissance, nous allons forcer ce nombre à se situer entre 1 et 10 – et nous ne pouvons pas utiliser exactement 10. Nous pouvons utiliser « 9,99999999… », mais pas « 10 ». En notation scientifique, le nombre ne peut avoir qu'un seul chiffre à gauche de la virgule.
Ça permet deux choses : cela nous évite d'avoir à écrire de longs nombres multipliés par 10 à une petite puissance, et on peut ensuite décider d’afficher ou d’arrondir tous les chiffres après la virgule, selon l’utilisation qu’on va faire du nombre. Même si ces nombres peuvent représenter de grandes quantités, dans le contexte global de ce nombre, ils ne représentent pas des quantités aussi importantes que ce premier chiffre. On peut décider d’inclure les chiffres après la virgule si nécessaire, ou on peut les arrondir si ça nous convient. Par exemple, si une personne obtient le nombre 2,54382413, et que quelqu'un d'autre dit que c'est environ 2,5, c’est peut-être suffisamment précis. Qu’on dise 2,5×1012 ou 2,456838×1012, le résultat sera relativement similaire.
Dans l'exemple ci-dessus, où nous étions coincés avec 254 382 413×104, on peut maintenant parler de 2,54382413×1012, ou arrondir à 2,5×1012. C'est à nous de choisir.
Il suffit de déplacer la virgule!
Voici un autre exemple : 13 400. C'est « 134 », puis « 00 », ce qui signifie 134×102. Pour suivre notre règle, nous devons prendre ce 134 et le transformer en un nombre entre 1 et 10 – et tout ce que nous avons le droit de faire, c'est de déplacer la virgule. Donc, transformons-le en 1,34. C'est permis, car c'est un nombre entre 1 et 10. Pour ce faire, nous avons dû changer 134 en 1,34, ce qui revient à déplacer la virgule de deux places. (N'oubliez pas que de manière implicite, la virgule est placée après le 4 dans le nombre 134.) Comme nous avons déplacé la virgule décimale de deux places et réduit le 134, nous devons compenser en augmentant la puissance de dix. Ainsi, notre 134×102 du début est devenu 1,34×104, et c'est une notation scientifique correcte. C'est aussi exactement ce qu'est 13 400 : 1,34 « dix milles » (puisque 10 000 est 104).
Si on arrondit, ce nombre devient 1×104 : un « 1 » suivi de quatre zéros. Mais ces zéros ne sont plus vraiment des zéros, ce sont des places tenues par d'autres chiffres. Mais la notation accomplit la même chose que s'il s'agissait de zéros. Les quatre places après le « 1 » sont toujours quatre places valides, et donc l’exposant « quatre » devient la puissance que nous pouvons appliquer au 10. C'est ce qui est important pour le concept de la notation scientifique.
Autres puissances
Et maintenant, qu'en est-il des petits nombres? On peut faire exactement la même chose, sauf que cette fois, nos très petits nombres n'auront pas de zéros après – les zéros seront devant. Prenons un exemple simple : 0,005, qui s'écrit en noms « cinq millièmes » :
La partie numérique de ce nombre décimal va devenir un 5 en notation scientifique, mais nous devons trouver quelle puissance de dix lui donner. Cette virgule après le 5 a dû être déplacée de trois places vers la gauche pour arriver à 0,005. Donc, une fois de plus, nous allons équilibrer les choses en utilisant l’exposant qui correspond au nombre de bonds vers la gauche qu’a dû faire la virgule. Mais nous ne pouvons pas utiliser 3, parce que 5×103 serait 5 milles. Notre nombre est 5 millièmes. On comprend que puisque la virgule a été déplacée vers la gauche, il faut utiliser une puissance négative : notre puissance de dix sera 10-3. En général, ce sera toujours le cas - si votre nombre de départ est supérieur à 1, votre puissance de dix sera positif. Si le nombre est inférieur à 1, l’exposant sera négatif.
Un autre exemple - que diriez-vous du bon vieux 1/2, c’est-à-dire 0,5? Encore une fois, ce nombre utilise un 5, et nous avons dû déplacer la virgule d'une place vers la gauche pour obtenir 0,5. Donc la puissance de dix dans ce cas doit être -1. En fait, quand vous étudiez l'algèbre, vous verrez que 10-1 est en fait 1/10. Donc 5×10-1 est précisément ce que son nom indique : cinq « dixièmes ». Et c'est 0,5, comme on le voulait.
Nous avons vu des exposants positifs et des exposants négatifs ; que diriez-vous d'utiliser 0 comme exposant? Lorsque vous étudierez les exposants, vous verrez que 100 est un nombre valide - c'est simplement 1. Avec un nombre comme 6,7, qui se situe déjà entre 1 et 10, la notation scientifique n'y changera rien. Nous n'avons pas du tout besoin de déplacer la virgule - ou en d’autres mots, nous devons déplacer la virgule de zéro place. Nous pouvons donc écrire notre nombre sous la forme 6,7×100. Il s'agit en fait de 6,7 × 1, ce qui correspond à 6,7. C'est assez simple.
[Notons également que même si les puissances fractionnaires de 10 sont autorisées en mathématiques, nous ne les utilisons pas en notation scientifique.]
Dans le diagramme, vous avez un moyen de contrôler à la fois la partie numérique et la puissance de dix de votre notation scientifique. Vous ne pouvez utiliser que des exposants allant de -18 à +20, parce que nous voulons vous montrer le nombre écrit en entier, et c'est l’espace maximum que nous avions à l'écran. La notation scientifique peut en effet avoir des puissances de dix bien supérieures à 20 et bien inférieures à -18. En fait, elle peut être aussi grande ou aussi petite que vous le souhaitez. Mais arrivé à un certain point, les chiffres perdent leur sens physique. Il n'y a « que » 1080 atomes dans l'univers, selon la dernière théorie, alors c’est dur d’imaginer ce qu’on pourrait modéliser avec des puissances supérieures à cela. (Mais n'est-ce pas là justement une excellente justification d’utiliser la notation scientifique?!) Vous pouvez certainement utiliser de plus grands exposants, mais vous devrez avoir une bonne explication de ce que vous décrivez.
Quelque chose de plus
Nous faisons une petite parenthèse pour vous dire qu'il y a des nombres en mathématiques (surtout dans la théorie des nombres) qui sont beaucoup plus grands que ce que la notation scientifique standard peut montrer. Comment est-ce possible? Si vous essayez d'écrire le nombre d'atomes dans l'univers, il faudra écrire un nombre avec environ 80 zéros. C'est assez long, mais c’est possible. Et si vous vouliez avoir un nombre comportant autant de zéros qu'il y a d'atomes dans l'univers? Impossible d’écrire cela en notation scientifique, car vous n'auriez pas assez de papier ou d'encre (ou de temps) pour écrire la puissance astronomique de dix dont vous auriez besoin. Les mathématiciens ont conçu d'autres systèmes numériques qu'ils utilisent pour parler de nombres vraiment gigantesques comme ceux-ci. Souvent, les mathématiciens ne s'occupent pas des objets qui existent dans le monde physique. Ça veut dire qu'ils n'ont pas de limites quant à la taille des nombres qu'ils peuvent utiliser dans leurs démonstrations, ou dans tout ce à quoi les mathématiciens peuvent penser.
Revenons à la notation scientifique
Nous vous avons donné deux curseurs. En déplaçant les curseurs, vous verrez le grand nombre changer en conséquence. En dessous, vous verrez également la notation scientifique correspondante changer. Vous contrôlez la notation scientifique, et le grand nombre suit pas à pas. Vous pouvez créer n'importe quel nombre dans cette plage (à condition qu'il ne comporte pas plus de trois chiffres significatifs) en plaçant les curseurs où vous le voulez.
Vous avez également une case à cocher pour la « notation ingénieur ». Qu'est-ce que c'est? Eh bien, si vous avez étudié le système métrique, vous savez qu'il y a des préfixes multiplicateurs ou diviseurs que l'on peut ajouter sur n'importe quelle unité. Ces préfixes commencent assez simplement, avec des préfixes pour 10, 100, 1/10, 1/100. Mais ensuite, il y en a aussi pour 1 000 et 1/1000, 1 000 000 et 1/1000000, et ainsi de suite. Lorsque vous comptez le nombre de zéros que ces préfixes représentent, vous passez d’un préfixe à l'autre en changeant le nombre de zéros par multiple de trois. Les préfixes sont définis loin dans les deux sens, mais ils représentent toujours des nombres qui sautent à chaque fois de trois zéros.
Nous préférons presque toujours utiliser ces préfixes ; nous ne voulons pas dire 1×10-6 mètres, mais plutôt 1 micromètre (μm). Nous voulons dire 1 gigawatt (GW), millikelvin (mK), kilopieds (kpi), ou téradollar (T$) – et nous voulons utiliser les préfixes plutôt que des puissances de dix. Ces puissances de dix sont toutes des multiples de trois, nous ne voulons donc pas nous retrouver avec un nombre comme 1×104. Il n'y a pas de préfixe multiplicateur pour 104, mais il y en a un pour 103. Donc, au lieu de dire 1×104, nous préférons dire 10×103 pour pouvoir utiliser un préfixe métrique multiplicateur. (Pour arriver à cette conversion, nous avons augmenté la partie numérique de 1 à 10, donc nous avons équilibré cela en réduisant la puissance de dix de 4 à 3). Maintenant, nous pouvons dire « kilo-n’importe quoi »! Cet exemple pourrait être 1×104 watts, mais nous pouvons maintenant dire simplement 10 kilowatts. La notation scientifique qui nous oblige à utiliser des puissances de dix qui sont des multiples de trois (pour pouvoir utiliser un préfixe multiplicateur ou diviseur approprié) s'appelle la notation ingénieur. La puissance de dix que nous devons utiliser est le multiple de trois égal ou inférieur à la puissance normale de dix que l'on trouve dans la notation scientifique standard. On abandonne maintenant la règle selon laquelle la partie numérique de notre chiffre doit se situer entre 1 et 10, afin de profiter des avantages d’un préfixe métrique. (Mais le chiffre doit toujours être compris entre 1 et 1 000!)
Donc si on avait 108, on réduirait à 106 pour pouvoir utiliser le préfixe multiplicateur « méga ». 10-2 deviendrait 10-3, ou « milli- ». 10-7 deviendrait 10-9, ou « nano- ».
Ce que vous pouvez apprendre :
- Vous pouvez apprendre ce que sont les « puissances de dix »
- Vous pouvez comprendre pourquoi les très grands et les très petits nombres sont notés de manière à éviter d’écrire beaucoup de zéros
- Vous pouvez apprendre à convertir des nombres en utilisant différentes puissances de dix
- Vous pouvez vous initier à l'utilisation des nombres négatifs - et même de zéro - comme puissance de dix
- Vous pouvez apprendre qu'il existe une variante de la notation scientifique appelée notation ingénieur, qui vous permet d'utiliser des préfixes métriques standard
- Vous pouvez apprendre qu'il existe des systèmes de notation pour les nombres qui sont trop grands ou trop petits, même pour la notation scientifique